Всероссийская олимпиада школьников по математике, 10 класс, 2019 год
дата проведения: 14 октября 2019 - 20 октября 2019
Задача 5.
Внутри квадрата $ABCD$ отмечены точки $K$ и $M$ (точка $M$ находится внутри треугольника $ABD$, точка $K$ — внутри $BMC$) так, что треугольники $BAM$ и $DKM$ равны ($AM$ = $KM$, $BM$ = $MD$, $AB$ = $KD$). Найдите $∠KCM$, если $∠AMB$ = 100°.
Ответ на Задачу 5.
Ответ: 35°.
Решение:
Заметим, что треугольники $ABM$ и $AMD$ также равны по трём сторонам. Таким образом, точка $M$ лежит на диагонали $AC$ квадрата, то есть $∠MCD$ = $∠MAD$ = $∠MAB$ = 45° (см. рисунок).
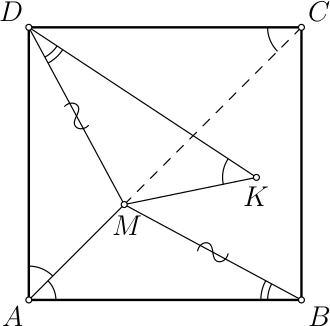
Кроме этого, из равенства треугольников $BAM$ и $DKM$ следует, что $∠MKD$ = $∠BAM$ = 45°. Получается, что четырёхугольник $MKCD$ — вписанный. Тогда $∠KCM$ = $∠KDM$ = 180° − 100° − 45° = 35°.

