Двое рабочих за два часа вырыли траншею. При этом первый рабочий устал и начал работать втрое медленней, а второй рабочий раззадорился и начал работать втрое быстрее, так что на прокладку второй такой траншеи у них ушёл один час. Во сколько раз производительность второго превосходила производительность первого изначально?

В прямоугольном треугольнике один катет в два раза больше другого. Разрежьте его на 5 равных треугольников.

Над девятизначным числом разрешается производить следующее действие: любую цифру числа можно заменить на последнюю цифру суммы цифр этого числа. Можно ли с помощью таких действий из числа 133355555 получить число 123456789?

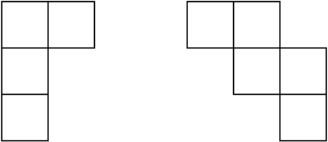
Квадрат 6 × 6 разрезали на четырёхклеточные и пятиклеточные фигуры, равные показанным на рисунке (обе фигуры участвуют в разрезании). Сколько каких фигур было использовано?

Внутри квадрата $ABCD$ отмечены точки $K$ и $M$ (точка $M$ находится внутри треугольника $ABD$, точка $K$ — внутри $BMC$) так, что треугольники $BAM$ и $DKM$ равны ($AM$ = $KM$, $BM$ = $MD$, $AB$ = $KD$). Найдите $∠KCM$, если $∠AMB$ = 100°.

Даны квадратные трёхчлены $x^2 + ax + b$, $x^2 + cx + d$ и $x^2 + ex + f$. Оказалось, что любые два из них имеют общий корень, но все три общего корня не имеют. Докажите, что выполнены ровно два неравенства из следующих трёх:

$\displaystyle \frac{a^2 + c^2 − e^2}{4}>b + d − f$

$\displaystyle \frac{c^2 + e^2 − a^2}{4}>d + f − b$

$\displaystyle \frac{e^2 + a^2 − c^2}{4}>f + b − d$