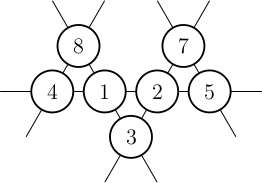
Задача 8.
Серёжа расставил в кружочках числа от 1 до 8 так, что каждое из чисел, кроме одного, использовано ровно по одному разу. Оказалось, что суммы чисел на каждой из пяти линий равны. Какое число Серёжа не использовал?
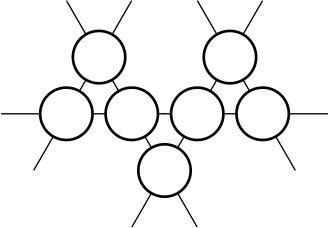
Ответ на Задачу 8.
Ответ: 6.
Решение:
Заметим, что каждое число содержится ровно в двух линиях. Поэтому удвоенная сумма всех использованных чисел в пять раз больше, чем сумма чисел на одной линии. Значит, сумма всех чисел делится на 5.
Заметим, что 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36. Поэтому, чтобы сумма использованных чисел делилась на 5, Серёжа должен отказаться от использования единицы или шестёрки.
Если Серёжа не будет использовать единицу, то сумма чисел в каждом ряду будет равна (2 + 3 + 4 + 5 + 6 + 7 + 8) · 2 : 5 = 14. Но у нас есть два ряда, содержащие по два числа, а 14 можно представить в виде суммы двух рассматриваемых цифр лишь одним способом: 14 = 6 + 8.
Значит, Серёжа не использует цифру 6. Например, он может справиться с поставленной задачей следующим образом: