Бумажный прямоугольник 3×7 разрезали на квадратики 1×1. Каждый квадратик, за исключением тех, что стояли в углах прямоугольника, разрезали по обеим диагоналям. Сколько получилось маленьких треугольников?

Алла загадала трёхзначное число, в котором нет цифры 0, и все цифры различны. Белла записала число, в котором те же цифры идут в обратном порядке. Галя вычла из большего числа меньшее. Какая цифра стоит у полученной разности в разряде десятков?

У Маши есть 4 куска пластилина красного цвета, 3 куска пластилина синего цвета и 5 кусков пластилина жёлтого цвета. Сначала она разделила пополам каждый не красный кусок пластилина, а затем разделила пополам каждый не жёлтый кусок пластилина. Сколько кусков пластилина получила Маша?

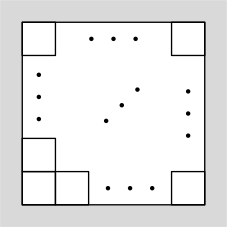
Квадратную площадку замостили квадратной плиткой (все плитки одинаковые). К четырём сторонам площадки примыкает в общей сложности 20 плиток. Сколько всего плиток использовалось?

Мерлин решил взвесить короля Артура на заколдованных весах, которые всегда ошибаются на один и тот же вес в одну и ту же сторону. Когда Мерлин взвесил Артура, они показали вес 19 стоунов. Затем Мерлин взвесил королевского коня и получил вес 101 стоун. Наконец, Мерлин взвесил Артура на коне, и весы показали 114 стоунов. Сколько стоунов весит король Артур на самом деле?

У Петра есть 5 клеток с кроликами (клетки стоят в один ряд). Известно, что в каждой клетке сидит хотя бы один кролик. Будем называть двух кроликов соседями, если они сидят либо в одной клетке, либо в соседних. Оказалось, что у каждого кролика есть либо 3, либо 7 соседей. Сколько кроликов сидит в центральной клетке?

В очереди в школьную столовую стоят 16 школьников так, что мальчики и девочки среди них чередуются. (Первым стоит мальчик, за ним — девочка, за ней — снова мальчик и так далее.) Любой мальчик, за которым в очереди стоит девочка, может поменяться с ней местами. Через некоторое время оказалось, что все девочки стоят в начале очереди, а все мальчики — в конце. Сколько обменов было совершено?

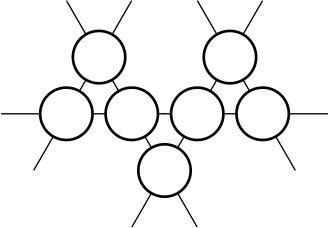
Серёжа расставил в кружочках числа от 1 до 8 так, что каждое из чисел, кроме одного, использовано ровно по одному разу. Оказалось, что суммы чисел на каждой из пяти линий равны. Какое число Серёжа не использовал?