Всероссийская олимпиада школьников по математике, 10 класс, 2020 год
дата проведения: 21 октября 2020 - 23 октября 2020
источник: https://olympiads.mccme.ru/vmo/
Задача 1.
В каждую клетку таблицы 5 × 5 невидимыми чернилами вписано натуральное число. Известно, что сумма всех чисел равна 200, а сумма трёх чисел, находящихся внутри любого прямоугольника 1 × 3, равна 23. Чему равно центральное число в таблице?
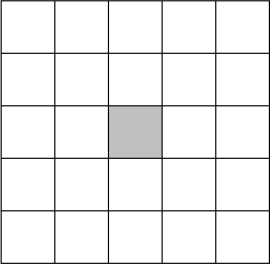
Ответ на Задачу 1.
Ответ: 16.
Решение:
Разобьём квадрат 5 × 5 без центральной клетки на четыре прямоугольника 2 × 3, а каждый из них разобьём на два прямоугольника 1 × 3.
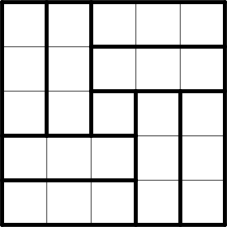
Получится 8 прямоугольников 1 × 3, сумма чисел в каждом из которых равна 23. Поскольку сумма вообще всех чисел равна 200, находим число в центральной клетке как 200 − 23 ⋅ 8 = 16.
