Задача 1.
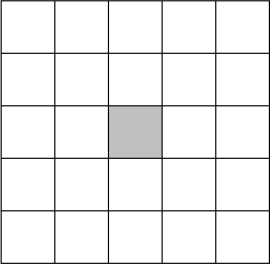
В каждую клетку таблицы 5 × 5 невидимыми чернилами вписано натуральное число. Известно, что сумма всех чисел равна 200, а сумма трёх чисел, находящихся внутри любого прямоугольника 1 × 3, равна 23. Чему равно центральное число в таблице?
Задача 2.
Известно, что $\displaystyle \frac{a + b}{a − b} = 3$. Найдите значение выражения $\displaystyle \frac{a^2 − b^2}{a^2 + b^2}$.
Задача 3.
У Юры есть 𝑛 карточек, на которых написаны числа от 1 до 𝑛. После того, как Юра потерял одну из них, сумма чисел на оставшихся оказалась равна 101. Какое число написано на потерянной карточке?
Задача 4.
В центральной клетке доски 21 × 21 находится фишка. За один ход можно передвинуть фишку в соседнюю по стороне клетку. Алина сделала 10 ходов. Сколько существует клеток, где может оказаться фишка?
Задача 5.
Хулиган Вася любит бегать по эскалатору в метро, причём вниз он бежит в два раза быстрее, чем вверх. Если эскалатор не работает, то, чтобы сбегать вверх и вниз, Васе потребуется 6 минут. Если эскалатор едет вниз, то, чтобы сбегать вверх и вниз, Васе потребуется 13,5 минут. Сколько секунд потребуется Васе, чтобы сбегать вверх и вниз по эскалатору, который будет ехать вверх? (Эскалатор всегда движется с постоянной скоростью.)
Задача 6.
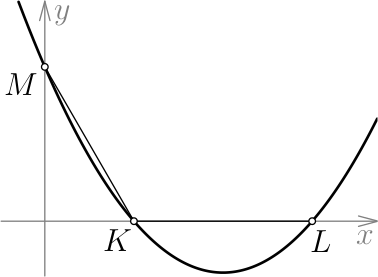
График квадратного трёхчлена $\displaystyle 𝑦 = \frac{2}{\sqrt{3}}𝑥^2 + 𝑏𝑥 + 𝑐$ пересекает оси координат в трёх точках 𝐾, 𝐿 и 𝑀, как на рисунке ниже. Оказалось, что 𝐾𝐿 = 𝐾𝑀 и ∠𝐿𝐾𝑀 = 120°. Найдите корни данного трёхчлена.
Задача 7.
У Олега есть четыре карточки, на каждой из которых с одной и с другой стороны написаны натуральные числа (всего написано 8 чисел). Он рассматривает всевозможные четвёрки чисел, где первое число написано на первой карточке, второе — на второй, третье — на третьей, четвёртое — на четвёртой. Затем для каждой четвёрки он выписывает произведение чисел к себе в блокнот. Чему равна сумма восьми чисел на карточках, если сумма шестнадцати чисел в блокноте Олега равна 330?
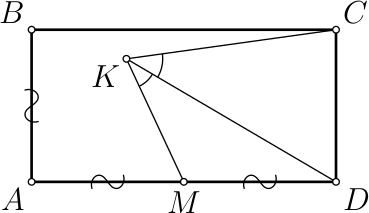
Задача 8.
Прямоугольник 𝐴𝐵𝐶𝐷 таков, что 𝐴𝐷 = 2𝐴𝐵. Точка 𝑀 — середина стороны 𝐴𝐷. Внутри прямоугольника нашлась точка 𝐾 такая, что ∠𝐴𝑀𝐾 = 80° и луч 𝐾𝐷 является биссектрисой угла 𝑀𝐾𝐶. Сколько градусов составляет угол 𝐾𝐷𝐴?