Задача 6.
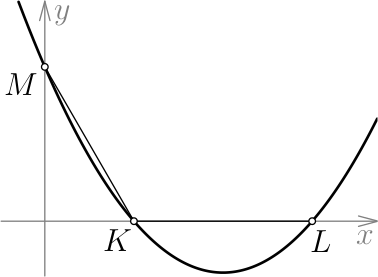
График квадратного трёхчлена $\displaystyle 𝑦 = \frac{2}{\sqrt{3}}𝑥^2 + 𝑏𝑥 + 𝑐$ пересекает оси координат в трёх точках 𝐾, 𝐿 и 𝑀, как на рисунке ниже. Оказалось, что 𝐾𝐿 = 𝐾𝑀 и ∠𝐿𝐾𝑀 = 120°. Найдите корни данного трёхчлена.
Ответ на Задачу 6.
Ответ: 0,5 и 1,5.
Решение:
Решение: Обозначим начало координат за 𝑂, а меньший корень за 𝑝 (тогда и длина отрезка 𝐾𝑂 равна 𝑝). По условию треугольник 𝑂𝑀𝐾 прямоугольный с углом 30° при вершине 𝑀, поэтому 𝑂𝑀 = $\sqrt{3}$𝐾𝑂 = $\sqrt{3}$𝑝 и 𝐾𝑀 = 2𝐾𝑂 = 2𝑝. Также по условию 𝐾𝐿 = 𝐾𝑀, поэтому 𝑂𝐿 = 𝑝 + 2𝑝 = 3𝑝, т.е. больший корень равен 3𝑝 (см. рисунок).

По теореме Виета произведение корней квадратного трёхчлена равно отношению свободного члена к старшему коэффициенту. Поскольку свободный член равен значению трёхчлена в нуле, т.е. длине отрезка 𝑂𝑀, получаем уравнение:
$\displaystyle p ⋅ 3p = \frac{\sqrt{3} p}{2 / \sqrt{3}}$
Решая его, получаем 𝑝 = 1,5. Следовательно, корни данного трёхчлена равны 𝑝 = 1,5 и 3𝑝 = 4,5.

