Задача 8.
Прямоугольник 𝐴𝐵𝐶𝐷 таков, что 𝐴𝐷 = 2𝐴𝐵. Точка 𝑀 — середина стороны 𝐴𝐷. Внутри прямоугольника нашлась точка 𝐾 такая, что ∠𝐴𝑀𝐾 = 80° и луч 𝐾𝐷 является биссектрисой угла 𝑀𝐾𝐶. Сколько градусов составляет угол 𝐾𝐷𝐴?
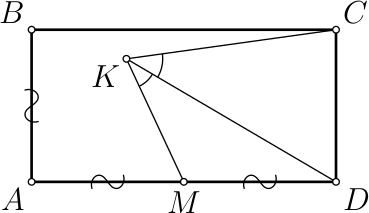
Ответ на Задачу 8.
Ответ: 35°.
Решение:
Начнём с предположения, что четырёхугольник 𝐾𝑀𝐷𝐶 является вписанным (далее будет предложено несколько доказательств данного факта).
Воспользовавшись тем, что во вписанном четырёхугольнике 𝐾𝑀𝐷𝐶 сумма противоположных углов равна 180°, получим ∠𝑀𝐾𝐷 = $\displaystyle \frac{∠𝑀𝐾𝐶}{2}$ = $\displaystyle \frac{180° − ∠𝑀𝐷𝐶}{2}$ = 45°. Угол 𝐴𝑀𝐾 как внешний для треугольника 𝐾𝐷𝑀 равен сумме углов 𝑀𝐾𝐷 и 𝐾𝐷𝐴, поэтому искомый угол 𝐾𝐷𝐴 равен 80° − 45° = 35°.
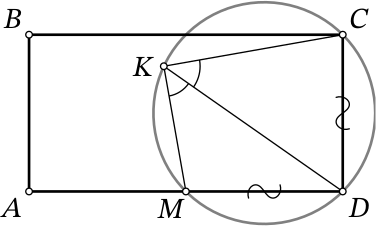
Приведём первое возможное доказательство вписанности четырёхугольника 𝐾𝑀𝐷𝐶. Рассмотрим треугольник 𝑀𝐾𝐶 и его описанную окружность. Заметим, что точка 𝐷 лежит на биссектрисе угла 𝑀𝐾𝐶, а также равноудалена от вершин 𝑀 и 𝐶 (см. рисунок). Но биссектриса угла неравнобедренного треугольника и серединный перпендикуляр к его противоположной стороне, как известно, пересекаются в середине «меньшей» дуги описанной окружности треугольника. Другими словами, 𝐷 — середина дуги 𝑀𝐶 описанной окружности треугольника 𝑀𝐾𝐶, не содержащей точку 𝐾. Надо также заметить, что 𝑀𝐾 ≠ 𝐾𝐶 (иначе треугольники 𝐾𝑀𝐷 и 𝐾𝐶𝐷 оказались бы равны, но ∠𝐾𝑀𝐷 > 90° > ∠𝐾𝐶𝐷).
Приведём второе возможное доказательство вписанности четырёхугольника 𝐾𝑀𝐷𝐶. Оно будет использовать четвёртый признак равенства треугольников: если у двух треугольников равны две стороны и угол не между ними, то эти треугольники либо равны, либо сумма других двух углов не между ними равна 180°. Четвёртый признак выполняется для треугольников 𝑀𝐷𝐾 и 𝐶𝐷𝐾 (𝑀𝐷 = 𝐷𝐶, 𝐷𝐾 — общая, ∠𝑀𝐾𝐷 = ∠𝐶𝐾𝐷). При этом углы 𝐾𝑀𝐷 и 𝐾𝐶𝐷 не равны (опять же, первый — тупой, а второй — острый), поэтому их сумма равна 180°, а это и есть противоположные углы четырёхугольника 𝐾𝑀𝐷𝐶. Следовательно, он является вписанным.

