Задача 6.
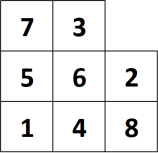
Впишите вместо букв 𝐴, 𝐵, 𝐶, 𝐷, 𝐸 цифры 1, 2, 3, 4, 5 так, чтобы сумма цифр во всех прямоугольниках 1 × 3 (и горизонтальных, и вертикальных) равнялась 13. Каждая из цифр от 1 до 5 должна встречаться в таблице ровно один раз.
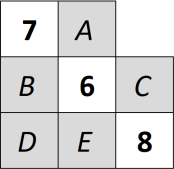
Ответ на Задачу 6.
Ответ: 𝐴, 𝐵, 𝐶, 𝐷, 𝐸 соответствуют 3, 5, 2, 1, 4.
Решение:
Сумма всех чисел в таблице равна 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36, а в каждом из первых двух столбцов она равна 13. Значит, общая сумма чисел в таблице равна 36 = 13 + 13 + (8 + 𝐶), откуда 𝐶 = 2.
Во второй строке сумма равна 13 = 𝐵 + 6 + 𝐶 = 𝐵 + 6 + 2, откуда 𝐵 = 5.
В первом столбце сумма равна 13 = 7 + 𝐵 + 𝐷 = 7 + 5 + 𝐷, откуда 𝐷 = 1.
В нижней строке сумма равна 13 = 𝐷 + 𝐸 + 8 = 1 + 𝐸 + 8, откуда 𝐸 = 4.
Во втором столбце сумма равна 13 = 𝐴 + 6 + 𝐸 = 𝐴 + 6 + 4, откуда 𝐴 = 3.
Итак, искомая расстановка имеет следующий вид: