Задача 1.
На доске были написаны четыре арифметических примера. Вера стёрла один знак «плюс», один знак «минус», один знак «умножить», один знак «делить», а также четыре знака «равно». Вместо одинаковых знаков она написала одинаковые буквы, а вместо разных знаков — разные буквы. Восстановите примеры.

Задача 2.
У Пети есть 25 монет, каждая из которых имеет номинал 1, 2, 5 или 10 рублей. Среди этих монет 19 — не двухрублёвые, 20 — не десятирублёвые, 16 — не однорублёвые. Сколько пятирублёвых монет у Пети?
Задача 3.
Термиты съели кусок старой деревянной шахматной доски. Сколько чёрных клеток они съели?
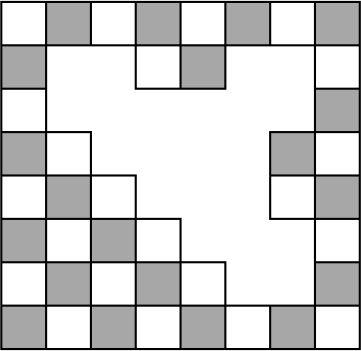
Задача 4.
В очереди в столовую стоят пять школьников: Аня, Боря, Вера, Гена и Денис.
- Боря стоит в начале очереди.
- Вера стоит рядом с Аней, но не рядом с Геной.
- Среди Ани, Бори и Гены никакие двое не стоят рядом.
Кто стоит рядом с Денисом?
Задача 5.
Антон загадал трёхзначное число, а Лёша пытается его угадать. Лёша по очереди назвал числа 109, 704 и 124. Антон заметил, что каждое из этих чисел совпадает с загаданным числом ровно в одном разряде. Какое число загадал Антон?
Задача 6.
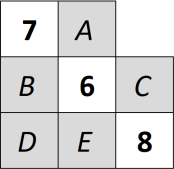
Впишите вместо букв 𝐴, 𝐵, 𝐶, 𝐷, 𝐸 цифры 1, 2, 3, 4, 5 так, чтобы сумма цифр во всех прямоугольниках 1 × 3 (и горизонтальных, и вертикальных) равнялась 13. Каждая из цифр от 1 до 5 должна встречаться в таблице ровно один раз.
Задача 7.
Денис кидал дротики в четыре одинаковых поля для дартса: в каждое поле он кинул ровно три дротика, куда они попали, показано на рисунке. На первом поле он набрал 30 очков, на втором — 38 очков, на третьем — 41 очко. Сколько очков он набрал на четвёртом поле? (За попадание в каждую определённую зону — кольцо или центральное поле — даётся определённое количество очков.)

Задача 8.
В роще растут деревья четырёх видов: берёзы, ели, сосны и осины. Всего 100 деревьев. Известно, что среди любых 85 деревьев найдутся деревья всех четырёх видов. Среди какого наименьшего количества любых деревьев в этой роще обязательно найдутся деревья хотя бы трёх видов?

