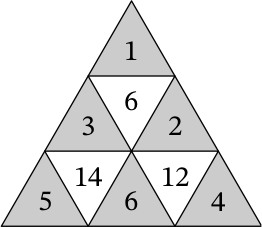
Задача 2.
Денис разбил треугольник на девять треугольничков, как показано на рисунке, и расставил в них числа, при этом в белых треугольниках числа оказались равны суммам чисел в соседних с ними (по сторонам) серых треугольниках. После этого Лёша стёр числа 1, 2, 3, 4, 5 и 6 и вместо них написал буквы 𝐴, 𝐵, 𝐶, 𝐷, 𝐸 и 𝐹 в некотором порядке. Получившаяся расстановка чисел и букв изображена на рисунке.
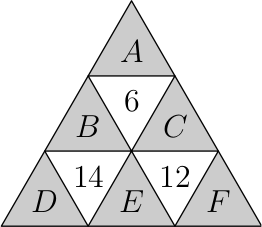
Где какие числа стояли первоначально?
Ответ на Задачу 2.
Ответ: Буквам 𝐴, 𝐵, 𝐶, 𝐷, 𝐸, 𝐹 соответствуют 1, 3, 2, 5, 6, 4.
Решение:
Заметим, что число 6 можно единственным образом представить в виде суммы трёх чисел из множества чисел от 1 до 6 — это 6 = 1 + 2 + 3 (или те же числа, но в другом порядке).
Теперь посмотрим на числа 𝐵, 𝐷 и 𝐸. Максимальное значение суммы 𝐷 + 𝐸 — это сумма 5 + 6 = 11, а максимальное значение 𝐵 равно 3. По условию сумма этих чисел в точности равна 14. Таким образом, 𝐵 = 3, 𝐷 и 𝐸 равны 5 и 6 (либо наоборот), 𝐴 и 𝐶 равны 1 и 2 (либо наоборот). Методом исключения получаем, что 𝐹 = 4.
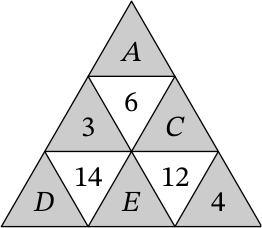
Максимальное значение суммы 𝐶 + 𝐸 — это сумма 6 + 2 = 8, а по условию 12 = 𝐶 + 𝐸 + 4. Отсюда мы уже однозначно восстанавливаем всю расстановку чисел.