Задача 1.
Петя записал на доску 20 натуральных чисел 1, 2, …, 20. Вася сначала стёр все чётные числа, а затем стёр все числа, дающие остаток 4 при делении на 5. Сколько чисел осталось на доске?
Задача 2.
Денис разбил треугольник на девять треугольничков, как показано на рисунке, и расставил в них числа, при этом в белых треугольниках числа оказались равны суммам чисел в соседних с ними (по сторонам) серых треугольниках. После этого Лёша стёр числа 1, 2, 3, 4, 5 и 6 и вместо них написал буквы 𝐴, 𝐵, 𝐶, 𝐷, 𝐸 и 𝐹 в некотором порядке. Получившаяся расстановка чисел и букв изображена на рисунке.
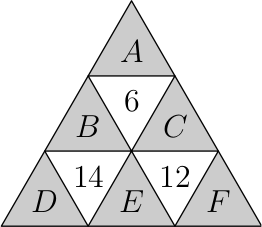
Где какие числа стояли первоначально?
Задача 3.
Листы в книге пронумерованы следующим образом: первый лист — это две страницы (с номерами 1 и 2), второй лист — это следующие две страницы (с номерами 3 и 4) и так далее. Хулиган Петя вырвал из книги несколько подряд идущих листов: первая вырванная страница имеет номер 185, а номер последней вырванной страницы состоит из тех же цифр, но идущих в другом порядке. Сколько листов вырвал Петя?
Задача 4.
На рисунке изображена фигура, состоящая из 17 клеток. Сколько существует способов разрезать её на 8 прямоугольников 1 × 2 и один квадратик 1 × 1?

Задача 5.
Прямоугольник разрезали на девять квадратов, как показано на рисунке. Длины сторон прямоугольника и всех квадратов — целые числа. Какое наименьшее значение может принимать периметр прямоугольника?
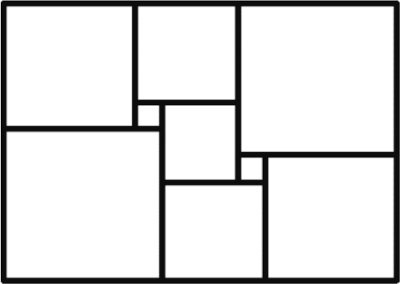
Задача 6.
Расстояние между городами А и Б составляет целое число километров. На дороге между городами каждый километр стоит табличка: на одной стороне написано расстояние до города А, на другой — до города Б. Слава шёл пешком из города А в город Б. В течение своего путешествия Слава посчитал для каждой таблички НОД чисел, написанных на ней. Оказалось, что среди посчитанных НОДов встречаются только числа 1, 3 и 13. Чему равняется расстояние между городами?
Задача 7.
В выборах на должность президента класса соревновались Петя и Вася. В течение трёх часов 27 учеников класса голосовали за одного из двух кандидатов. За первые два часа за Петю было отдано на 9 голосов больше, чем за Васю. А за последние два часа за Васю было отдано на 9 голосов больше, чем за Петю. В итоге Петя победил. С преимуществом в какое наибольшее количество голосов он мог победить?
Задача 8.
У Карлсона и Малыша есть несколько банок варенья, каждая весит целое число фунтов. Суммарный вес всех банок варенья Карлсона в 13 раз больше суммарного веса всех банок Малыша. Карлсон отдал Малышу банку с наименьшим весом (из тех, что были у него), после чего суммарный вес его банок оказался в 8 раз больше суммарного веса банок Малыша. Какое наибольшее количество банок варенья могло изначально быть у Карлсона?

