Задача 5.
Прямоугольник разрезали на девять квадратов, как показано на рисунке. Длины сторон прямоугольника и всех квадратов — целые числа. Какое наименьшее значение может принимать периметр прямоугольника?
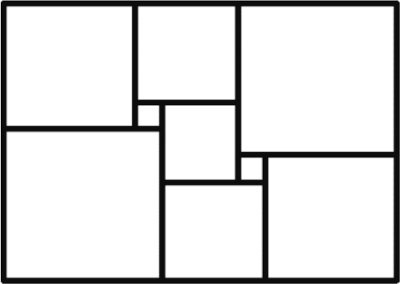
Ответ на Задачу 5.
Ответ: 52.
Решение:
Внутри квадрата будем писать длину его стороны. Обозначим стороны двух квадратов за 𝑎 и 𝑏 и будем последовательно вычислять длины сторон квадратов.
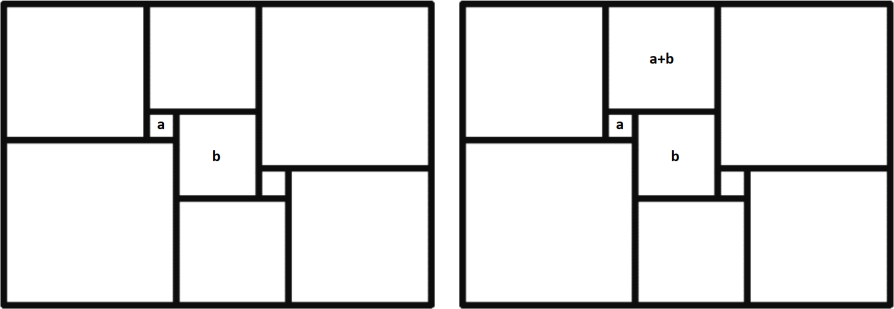
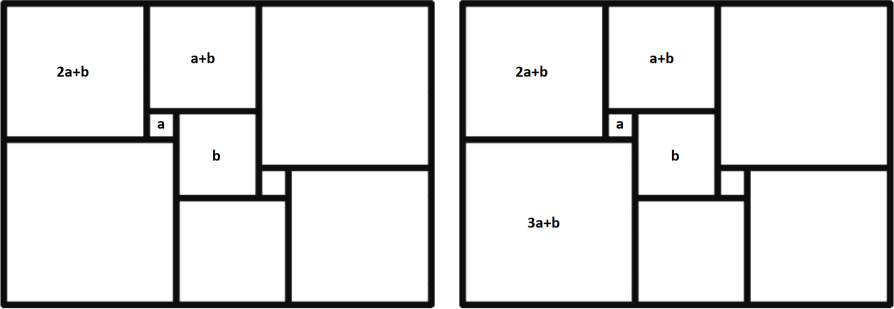
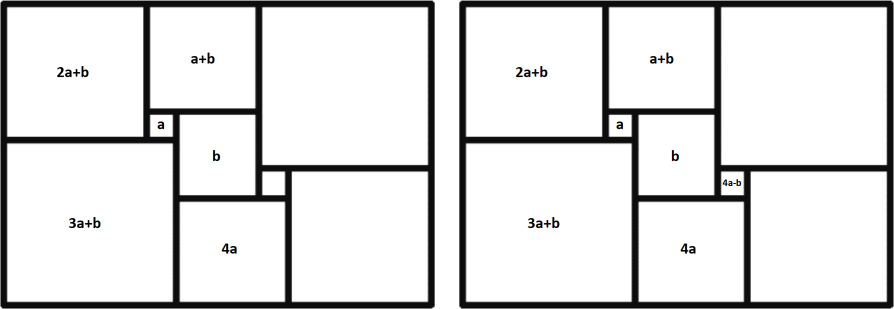
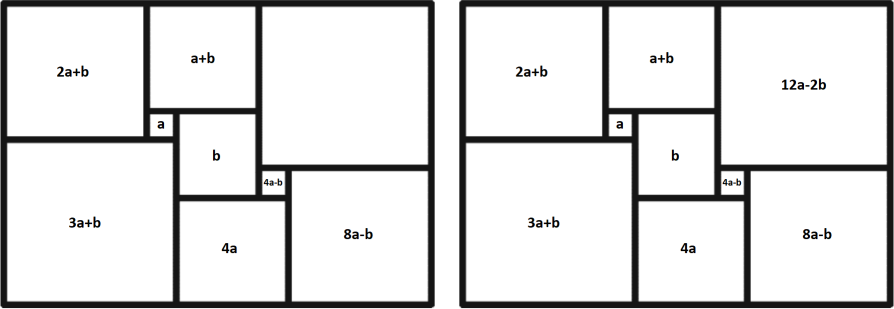
Сумма длин сторон двух квадратов, примыкающих к левой стороне прямоугольника, равна сумме длин сторон двух квадратов, примыкающих к правой стороне прямоугольника. Получаем уравнение:
(2𝑎 + 𝑏) + (3𝑎 + 𝑏) = (12𝑎 − 2𝑏) + (8𝑎 − 𝑏),
5𝑎 + 2𝑏 = 20𝑎 − 3𝑏,
𝑏 = 3𝑎.
Таким образом, чтобы минимизировать периметр прямоугольника, надо выбрать 𝑎 = 1, 𝑏 = 3. Несложно проверить, что при этих значениях прямоугольник будет иметь размеры 11 × 15, а его периметр будет равен 52.

