Задача 6.
Про четырёхугольник 𝐴𝐵𝐶𝐷 известно, что 𝐴𝐵 = 𝐵𝐷, ∠𝐴𝐵𝐷 = ∠𝐷𝐵𝐶, ∠𝐵𝐶𝐷 = 90°. На отрезке 𝐵𝐶 отмечена точка 𝐸 такая, что 𝐴𝐷 = 𝐷𝐸. Чему равна длина отрезка 𝐵𝐷, если известно, что 𝐵𝐸 = 7, 𝐸𝐶 = 5?
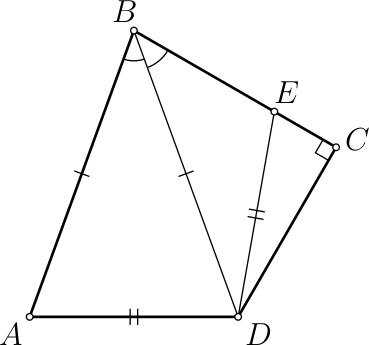
Ответ на Задачу 6.
Ответ: 17.
Решение:
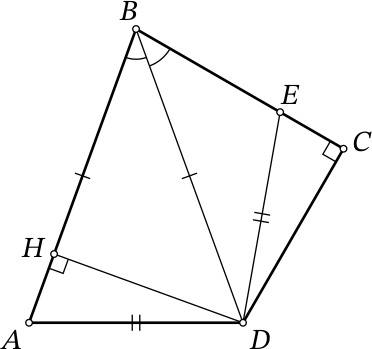
Опустим в равнобедренном треугольнике 𝐴𝐵𝐷 высоту из точки 𝐷, пусть 𝐻 — её основание (см. рисунок). Поскольку этот треугольник остроугольный (∠𝐴𝐵𝐷 = ∠𝐶𝐵𝐷 < 90°, ∠𝐵𝐴𝐷 = ∠𝐴𝐷𝐵 = $\displaystyle \frac{180° − ∠𝐴𝐵𝐷}{2}$ < 90°), точка 𝐻 лежит на отрезке 𝐴𝐵.
Заметим, что прямоугольные треугольники 𝐵𝐷𝐻 и 𝐵𝐷𝐶 равны по общей гипотенузе 𝐵𝐷 и острому углу при вершине 𝐵. Тогда 𝐵𝐻 = 𝐵𝐶 и 𝐷𝐻 = 𝐶𝐷.
Заметим теперь, что также равны прямоугольные треугольники 𝐴𝐷𝐻 и 𝐸𝐷𝐶 по гипотенузе 𝐴𝐷 = 𝐸𝐷 и катету 𝐷𝐻 = 𝐶𝐷. Тогда 𝐸𝐶 = 𝐴𝐻.
Итак, 𝐵𝐷 = 𝐵𝐴 = 𝐵𝐻 + 𝐴𝐻 = 𝐵𝐶 + 𝐸𝐶 = (7 + 5) + 5 = 17.

