Задача 1.
Квадрат разрезали на четыре равных прямоугольника, а из них сложили большую букву П (см. рисунок), периметр которой равен 56.
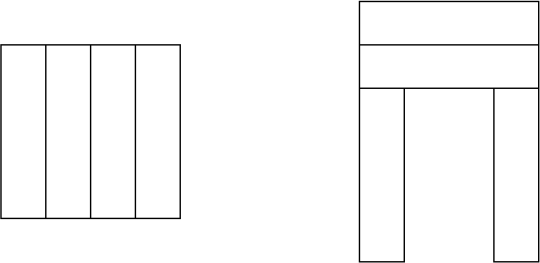
Чему равен периметр первоначального квадрата?
Задача 2.
Числа от 1 до 9 расставили в клетки таблицы 3 × 3 так, что сумма чисел на одной диагонали равна 7, а на другой — 21. Чему равна сумма чисел в пяти закрашенных клетках?

Задача 3.
Четверо ребят гуляли вдоль аллеи и решили посчитать количество елей, высаженных вдоль неё.
- Аня сказала: «Вдоль аллеи всего 15 елей.»
- Боря сказал: «Количество елей делится на 11.»
- Вера сказала: «Елей точно меньше 25.»
- Гена сказал: «А я уверен, что их количество делится на 22.»
Один мальчик и одна девочка сказали правду, а остальные двое ошиблись. Сколько елей растёт вдоль аллеи?
Задача 4.
В классе учатся 20 человек. Размышляя, каким девочкам отправить валентинку на 14 февраля, каждый мальчик составил список из всех симпатичных ему девочекодноклассниц (возможно, пустой). Известно, что не существует трёх мальчиков, у которых списки совпадают по количеству девочек. Какое наименьшее количество девочек может быть в классе?
Задача 5.
На бал пришли дамы и джентльмены — всего меньше 50 человек. Во время первого танца лишь четверть дам не были приглашены на танец, и 2/7 от общего количество джентльменов никого не пригласили. Сколько человек пришло на бал? (Для танца некоторый джентльмен приглашает некоторую даму.)
Задача 6.
Про четырёхугольник 𝐴𝐵𝐶𝐷 известно, что 𝐴𝐵 = 𝐵𝐷, ∠𝐴𝐵𝐷 = ∠𝐷𝐵𝐶, ∠𝐵𝐶𝐷 = 90°. На отрезке 𝐵𝐶 отмечена точка 𝐸 такая, что 𝐴𝐷 = 𝐷𝐸. Чему равна длина отрезка 𝐵𝐷, если известно, что 𝐵𝐸 = 7, 𝐸𝐶 = 5?
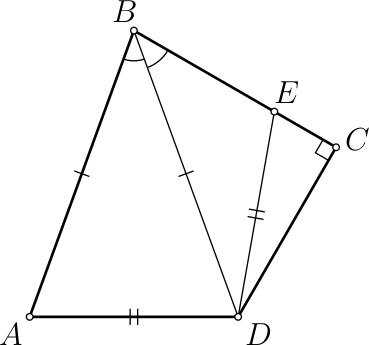
Задача 7.
Про три действительных числа $p$, $q$ и $r$ известно, что:
$\displaystyle p + q + r = 5,\quad\frac{1}{p + q} + \frac{1}{q + r} + \frac{1}{p + r} = 9.$
Чему равняется выражение:
$\displaystyle \frac{r}{p + q} + \frac{p}{q + r} + \frac{q}{p + r}$?
Задача 8.
Маша выписала на доску в порядке возрастания все натуральные делители некоторого числа 𝑁 (самый первый выписанный делитель — 1, самый большой выписанный делитель — само число 𝑁). Оказалось, что третий с конца делитель в 21 раз больше второго с начала. Какое наибольшее значение может принимать 𝑁?

