Задача 6.
На бал пришли 29 мальчиков и 15 девочек. Некоторые мальчики потанцевали с некоторыми девочками (не более одного раза в каждой паре). После бала каждый человек рассказал родителям, сколько раз он танцевал. Какое наибольшее количество различных чисел дети могли назвать?
Ответ на Задачу 6.
Ответ: 29 различных чисел.
Решение:
Наибольшее возможное число, которое могло быть названо, равно 29 (в случае, если есть девочка, которая потанцевала со всеми мальчиками), а наименьшее — 0. Таким образом, мы получили, что количество различных названных чисел не более 30.
Докажем, что ровно 30 быть не может. Предположим противное, пусть все числа от 0 до 29 были названы. Тогда числа от 16 до 29 названы только девочками (это уже 14 чисел). Число 0 назвал точно не мальчик, т.к. есть девочка, которая потанцевала со всеми мальчиками. Получается, что девочки должны назвать в точности пятнадцать чисел 0, 16, 17, 18, …, 29.
При этом число 15 не названо ни одной из девочек, т.к. уже известно, какие числа они называли. Если бы число 15 назвал мальчик, то это значило бы, что он потанцевал со всеми девочками. Но есть девочка, назвавшая число 0, которая ни с кем не танцевала. Противоречие.
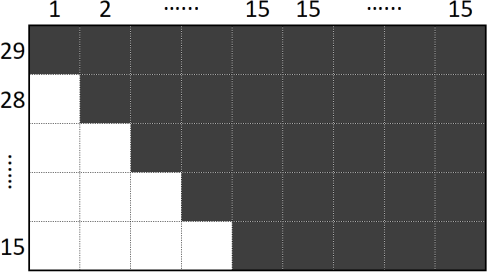
Теперь покажем, как могли быть названы 29 различных чисел. Пронумеруем девочек числами от 1 до 15, а мальчиков — числами от 1 до 29. Пусть мальчик 𝑖 потанцевал с девочкой 𝑗 в том и только в том случае, когда 𝑖 ≥ 𝑗.
Можно изобразить этот пример в виде таблицы 15 × 29: каждому мальчику поставим в соответствие столбец таблицы, каждой девочке — строку; если мальчик потанцевал с девочкой — будем закрашивать клетку на пересечении соответствующих строки и столбца. На рисунке над каждым столбцом написано, сколько в нём закрашенных клеток; слева от каждой строки написано, сколько в ней закрашено клеток.