Задача 1.
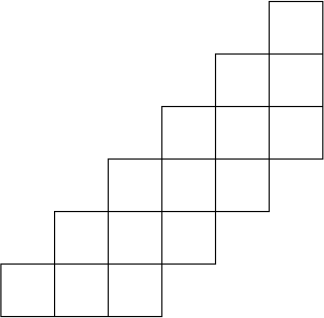
Фигуру, изображённую на рисунке, разрезали на одноклеточные квадраты и прямоугольники 1 × 2. Какое наибольшее количество прямоугольников 1 × 2 при этом могло получиться?
Задача 2.
Антон, Вася, Саша и Дима ехали на машине из города А в город Б, каждый из них по очереди был за рулём. Весь путь машина ехала с постоянной скоростью. Антон вёл машину в два раза меньше, чем Вася, а Саша вёл машину столько же, сколько Антон и Дима вместе взятые. Дима был за рулём лишь десятую часть пути. Какую часть пути за рулём был Вася? Ответ запишите в виде десятичной дроби.
Задача 3.
К 30 пальмам в разных частях необитаемого острова прибито по табличке.
- На 15 из них написано: «Ровно под 15 табличками зарыт клад».
- На 8 из них написано: «Ровно под 8 табличками зарыт клад».
- На 4 из них написано: «Ровно под 4 табличками зарыт клад».
- На 3 из них написано: «Ровно под 3 табличками зарыт клад».
Известно, что правдивы только те таблички, под которыми клада нет. Под каким наименьшим количеством табличек может быть зарыт клад?
Задача 4.
На рисунке слева направо изображены пересекающиеся квадраты со сторонами 12, 9, 7, 3 соответственно. На сколько сумма чёрных площадей больше, чем сумма серых площадей?
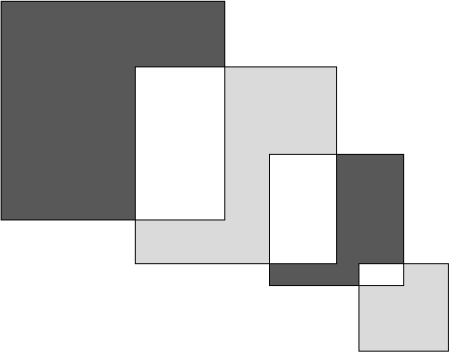
Задача 5.
У Буратино есть много монет по 5 и по 6 сольдо, каждого вида более 10 монет. Придя в магазин и купив книгу за 𝑁 сольдо, он понял, что не сможет за неё рассчитаться без сдачи. Какое наибольшее значение может принимать натуральное 𝑁, если оно не больше 50?
Задача 6.
На бал пришли 29 мальчиков и 15 девочек. Некоторые мальчики потанцевали с некоторыми девочками (не более одного раза в каждой паре). После бала каждый человек рассказал родителям, сколько раз он танцевал. Какое наибольшее количество различных чисел дети могли назвать?
Задача 7.
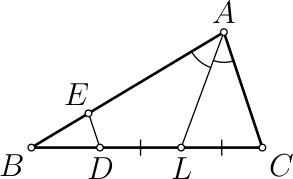
В треугольнике 𝐴𝐵𝐶 проведена биссектриса 𝐴𝐿. Точки 𝐸 и 𝐷 отмечены на отрезках 𝐴𝐵 и 𝐵𝐿 соответственно так, что 𝐷𝐿 = 𝐿𝐶, 𝐸𝐷 ∥ 𝐴𝐶. Найдите длину отрезка 𝐸𝐷, если известно, что 𝐴𝐸 = 15, 𝐴𝐶 = 12.
Задача 8.
Сколько существует пар натуральных чисел 𝑎 и 𝑏 таких, что 𝑎 ≥ 𝑏 и выполнено:
$\displaystyle \frac{1}{a} + \frac{1}{b} = \frac{1}{6}$ ?

