Всероссийская олимпиада школьников по математике, 9 класс, 2020 год
дата проведения: 21 октября 2020 - 23 октября 2020
источник: https://olympiads.mccme.ru/vmo/
Задача 7.
В треугольнике 𝐴𝐵𝐶 проведена биссектриса 𝐴𝐿. Точки 𝐸 и 𝐷 отмечены на отрезках 𝐴𝐵 и 𝐵𝐿 соответственно так, что 𝐷𝐿 = 𝐿𝐶, 𝐸𝐷 ∥ 𝐴𝐶. Найдите длину отрезка 𝐸𝐷, если известно, что 𝐴𝐸 = 15, 𝐴𝐶 = 12.
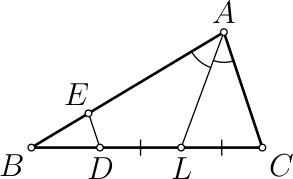
Ответ на Задачу 7.
Ответ: 3.
Решение:
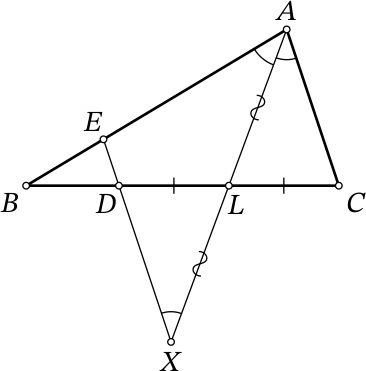
На луче 𝐴𝐿 за точкой 𝐿 отметим точку 𝑋 такую, что 𝑋𝐿 = 𝐿𝐴 (см. рисунок). Поскольку в четырёхугольнике 𝐴𝐶𝑋𝐷 диагонали точкой пересечения 𝐿 делятся пополам, он является параллелограммом (в частности, 𝐴𝐶 = 𝐷𝑋). Следовательно, 𝐷𝑋 ∥ 𝐴𝐶. Так как 𝐴𝐶 ∥ 𝐸𝐷 по условию, то точки 𝑋, 𝐷, 𝐸 лежат на одной прямой.
Поскольку 𝐴𝐶 ∥ 𝐸𝑋, то ∠𝐸𝐴𝑋 = ∠𝐶𝐴𝑋 = ∠𝐴𝑋𝐸, т.е. треугольник 𝐴𝐸𝑋 — равнобедренный, 𝐸𝐴 = 𝐸𝑋. Тогда:
𝐸𝐷 = 𝐸𝑋 − 𝑋𝐷 = 𝐸𝐴 − 𝐴𝐶 = 15 − 12 = 3.
