Задача 6.
На плоскости дана точка 𝑃. Какое наименьшее количество прямых, не проходящих через точку 𝑃, можно провести на плоскости так, чтобы любой луч с началом в точке 𝑃 пересекал хотя бы 170 выбранных прямых?
Ответ на Задачу 6.
Ответ: 341 прямая.
Решение:
Предположим, что проведено не более 340 прямых. Рассмотрим вспомогательную прямую ℓ, проходящую через точку 𝑃 и параллельную какой-нибудь из выбранных. Прямая ℓ пересекается не более чем с 339 прямыми, поэтому либо по одну, либо по другую сторону от точки 𝑃 она пересекается не более чем со 169 прямыми. Выбирая соответствующий луч на прямой ℓ, получаем противоречие. Следовательно, менее чем 341 прямой не обойтись.
Теперь приведём пример для 341 прямой. Рассмотрим окружность радиуса 1 с центром в точке 𝑃, впишем в неё правильный 341-угольник. Рассмотрим все «большие» диагонали этого 341-угольника (то есть такие диагонали, с одной стороны от которых 170 вершин многоугольника, а с другой — 169), и докажем, что множество прямых, содержащих эти диагонали, нам подходит. Для этого достаточно доказать, что любой луч, выходящий из 𝑃, пересекает хотя бы 170 диагоналей, а значит, и прямых, их содержащих.

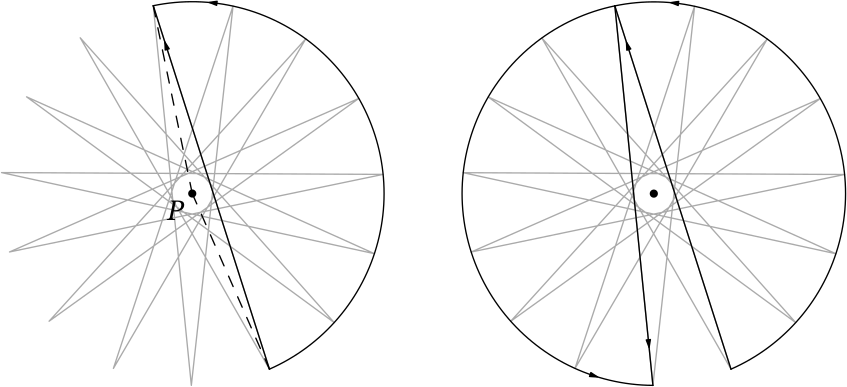
Заметим, что все эти диагонали объединяются в замкнутую ломаную с вершинами в вершинах исходного 341-угольника (пример аналогичной ломаной для 15-угольника приведён на рисунке выше). Эта ломаная «совершает вокруг точки 𝑃 ровно 170 оборотов», следовательно, любой луч, выходящий из точки 𝑃, ломаная должна пересечь не менее 170 раз, что даёт не менее 170 пересечений со звеньями ломаной (если луч проходит через вершину ломаной, то он пересекает оба отрезка с этой вершиной).
Приведём более строгие формулировку утверждения об оборотах ломаной и обоснование последующего вывода. Каждому звену ломаной можно сопоставить дугу описанной окружности нашего 341-угольника, которая видна из точки 𝑃 под тем же углом, что и само звено (первый рисунок ниже). Так как это звено есть «большая» диагональ 341-угольника, то градусная мера такой дуги равна 170 / 341 ⋅ 360°.
Дуги, соответствующие последовательным звеньям ломаной, стыкуются в обмотку окружности (второй рисунок выше). Таким образом, всей ломаной в целом сопоставляется замкнутая обмотка окружности с градусной мерой 341 ⋅ 170 / 341 ⋅ 360° = 170 ⋅ 360°, то есть 170 полных оборотов.
Следовательно, любой луч, выходящий из 𝑃, 170 раз пересечёт обмотку, а значит, не менее 170 раз пересечёт отдельные дуги (может получиться больше, если он пересечёт концы дуг). С другой стороны, из рисунка ясно, что если луч пересекает дугу, то он пересекает и соответствующую диагональ, а значит, и прямую, её содержащую.
Замечание: В качестве примера также можно было выбрать прямые, содержащие стороны правильного 341-угольника с центром в точке 𝑃.

