Саша уже неделю смотрит все серии интересного сериала подряд. Вчера Саша посмотрел 9 серий, а сегодня всего 6. Оказалось, что сумма номеров всех серий, просмотренных вчера, равна сумме номеров всех серий, просмотренных сегодня. Какой номер имеет последняя просмотренная Сашей серия? (Серии нумеруются последовательными натуральными числами, начиная с 1.)

В магазине продаются 15 видов шоколада. За неделю Андрей попробовал 6 видов, Борис — 11, а Денис — 13. Оказалось, что ни один вид шоколада не продегустировали все трое. Сколько видов шоколада попробовали и Андрей, и Борис?

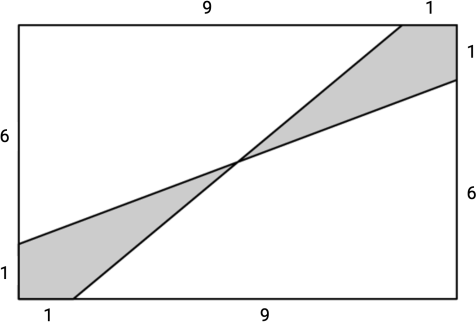
Дан прямоугольник 7 × 10. Чему равна площадь закрашенной фигуры?

В ряду чисел:

1, 2, 2, 3, 3, 3, 4, 4, 4, 4, …, 201, 201, …, 201

каждое число 𝑛 встречается ровно 𝑛 раз для всех 1 ⩽ 𝑛 ⩽ 201. Выберем в этом ряду такое число, слева и справа от которого чисел поровну. Определите это число.

Сумма трёх различных натуральных делителей нечётного натурального числа 𝑛 равна 10327. Какое наименьшее значение может принимать 𝑛?

На плоскости дана точка 𝑃. Какое наименьшее количество прямых, не проходящих через точку 𝑃, можно провести на плоскости так, чтобы любой луч с началом в точке 𝑃 пересекал хотя бы 170 выбранных прямых?

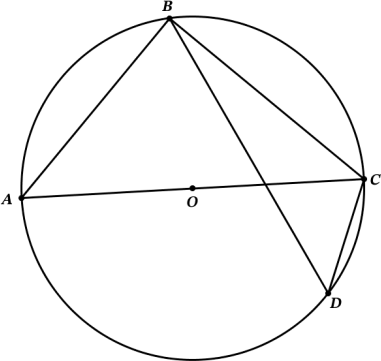
На окружности 𝜔 по разные стороны от диаметра 𝐴𝐶 расположены точки 𝐵 и 𝐷. Известно, что 𝐴𝐵 = 3$\sqrt{6}$, 𝐶𝐷 = 3, а площадь треугольника 𝐴𝐵𝐶 в три раза больше площади треугольника 𝐵𝐶𝐷. Найдите радиус окружности 𝜔.

Сколько существует троек натуральных чисел (𝑎, 𝑏, 𝑐), удовлетворяющих равенству:

max(𝑎, 𝑏) ⋅ max(𝑐, 12) = min(𝑎, 𝑐) ⋅ min(𝑏, 24)