Задача 7.
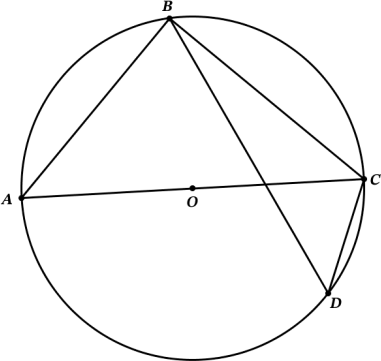
На окружности 𝜔 по разные стороны от диаметра 𝐴𝐶 расположены точки 𝐵 и 𝐷. Известно, что 𝐴𝐵 = 3$\sqrt{6}$, 𝐶𝐷 = 3, а площадь треугольника 𝐴𝐵𝐶 в три раза больше площади треугольника 𝐵𝐶𝐷. Найдите радиус окружности 𝜔.
Ответ на Задачу 7.
Ответ: 4,5.
Решение:
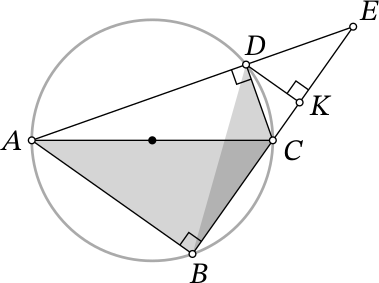
Заметим, что ∠𝐴𝐵𝐶 = ∠𝐴𝐷𝐶 = 90°, поскольку 𝐴𝐶 — диаметр. Опустим из точки 𝐷 перпендикуляр на 𝐵𝐶, пусть его основание — точка 𝐾 (см. рисунок). Так как площадь треугольника 𝐴𝐵𝐶 в 3 раза больше площади треугольника 𝐵𝐶𝐷, 𝐷𝐾 = 31 𝐴𝐵 = $\sqrt{6}$. Из прямоугольного треугольника 𝐷𝐶𝐾 по теореме Пифагора получаем:
$$ C K=\sqrt{C D^2-D K^2}=\sqrt{9 − 6}=\sqrt{3} $$
Продлим прямые 𝐵𝐶 и 𝐴𝐷 до пересечения в точке 𝐸 (эти прямые не параллельны, так как иначе 𝐴𝐷𝐾𝐵 был бы параллелограммом, но 𝐷𝐾 ≠ 𝐴𝐵). Так как 𝐷𝐾 — высота в прямоугольном треугольнике 𝐶𝐷𝐸, то 𝐷𝐾 2 = 𝐶𝐾 ⋅ 𝐸𝐾. Таким образом, 𝐸𝐾 = 2$\sqrt{3}$.
Заметим, что прямоугольные треугольники 𝐴𝐵𝐸 и 𝐷𝐾𝐸 подобны по острому углу. Отсюда 𝐵𝐸 ∶ 𝐾𝐸 = 𝐴𝐵 ∶ 𝐷𝐾 = 3 ∶ 1, то есть 𝐵𝐸 = 6$\sqrt{3}$. Получаем, что 𝐵𝐶 = 𝐵𝐸 − 𝐶𝐾 − 𝐾𝐸 = 3$\sqrt{3}$.
Остается ещё раз применить теорему Пифагора, получив:
𝐴𝐶2 = 𝐴𝐵2 + 𝐵𝐶2 = 54 + 27 = 81
откуда искомый радиус равен $\sqrt{81}$ / 2 = 4,5.

