Задача 6.
Женя взял доску 3 × 3 и на каждую клетку поставил столбик из синих и красных кубиков. Потом он зарисовал схему получившейся расстановки: подписал количество кубиков обоих цветов в каждом столбике (порядок кубиков неизвестен).
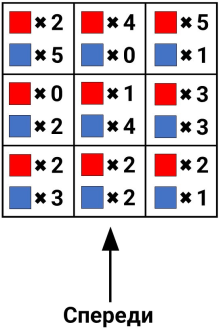
Какое наибольшее количество синих кубиков может увидеть Женя, если посмотрит на конструкцию спереди? (Например, если перед столбиком из 8 кубиков стоит столбик из 5, то будет видно все 5 кубиков ближнего столбика и только 3 верхних кубика дальнего столбика.)
Ответ на Задачу 6.
Ответ: 12 синих кубиков.
Решение:
Поймём, какое наибольшее количество синих кубиков Женя может увидеть в каждом из трёх рядов: левом, среднем и правом.
Левый ряд. Первый столбик состоит из 5 кубиков (2 красных и 3 синих), поэтому он полностью загораживает второй столбик, а также 5 из 7 кубиков последнего столбика. Таким образом, Женя видит все кубики первого столбика (среди них 3 синих), а также 2 кубика из последнего столбика (они оба могут быть синими). То есть в этом ряду он увидит максимум 3 + 2 = 5 синих кубиков.
Средний ряд. Первый столбик состоит из 4 кубиков (2 красных и 2 синих), поэтому он полностью загораживает последний столбик, а также 4 из 5 кубиков второго столбика. Таким образом, Женя видит все кубики первого столбика (среди них 2 синих), а также 1 кубик из второго столбика (он может быть синим). То есть в этом ряду он увидит максимум 2 + 1 = 3 синих кубика.
Правый ряд. Первый столбик состоит из 3 кубиков (2 красных и 1 синий), поэтому он загораживает 3 из 6 кубиков второго столбика. При этом второй столбик полностью загораживает последний столбик. Таким образом, Женя видит все кубики первого столбика (среди них 1 синий), а также 3 кубика из второго столбика (все три могут быть синими). То есть в этом ряду он увидит максимум 1 + 3 = 4 синих кубика.
Суммарно Женя увидит максимум 5 + 3 + 4 = 12 синих кубиков.

