Задача 1.
Круглые гири весят 200 грамм, квадратные — 300 грамм, а треугольные — 150 грамм. 12 гирь положили на чашечные весы, как показано на рисунке. Какая чаша тяжелее и на сколько грамм?
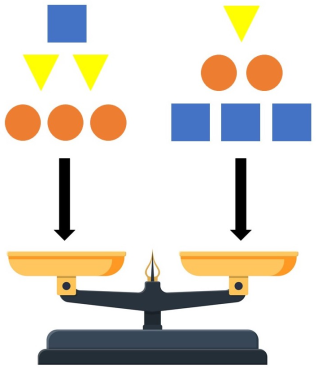
Задача 2.
В 4«А» классе у каждого ребёнка есть не менее 11 одноклассников и не менее 13 одноклассниц. Какое наименьшее количество детей может учиться в этом классе?
Задача 3.
У Саши было 47 палочек. Использовав их все, он сложил несколько букв «Б» и «В», изображённых на рисунке. Какое наибольшее количество букв «Б» могло получиться у Саши?

Задача 4.
Коты Леопольд, Гарфилд, Василий, Матильда и Том съели на кухне две котлеты, две сосиски и одну рыбу. Каждый из них съел что-то одно. Известно, что:
- Леопольд, Гарфилд и Том съели 3 разных блюда;
- Василий не ел котлету, а Леопольд не ел сосиску;
- Гарфилд и Матильда съели одно и то же.
Кому что досталось?
Задача 5.
У мамы с папой есть двое детей: Коля и Таня. Папа старше мамы на 4 года. Коля тоже старше Тани на 4 года и вдвое младше папы. Сколько лет каждому из них, если суммарный возраст всех членов семьи составляет 130 лет?
Задача 6.
Женя взял доску 3 × 3 и на каждую клетку поставил столбик из синих и красных кубиков. Потом он зарисовал схему получившейся расстановки: подписал количество кубиков обоих цветов в каждом столбике (порядок кубиков неизвестен).
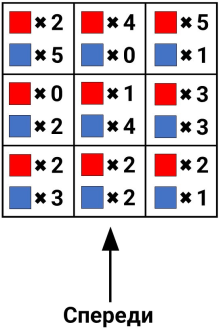
Какое наибольшее количество синих кубиков может увидеть Женя, если посмотрит на конструкцию спереди? (Например, если перед столбиком из 8 кубиков стоит столбик из 5, то будет видно все 5 кубиков ближнего столбика и только 3 верхних кубика дальнего столбика.)
Задача 7.
На столе лежит 4 стопки монет. В первой стопке 9 монет, во второй — 7, в третьей — 5, в четвёртой — 10. За один ход разрешается добавить по одной монете к трём разным стопкам. За какое наименьшее количество ходов можно добиться того, чтобы во всех стопках стало поровну монет?
Задача 8.
У Васи есть шесть одинаковых игральных кубиков, на гранях каждого из которых записаны числа от 1 до 6 (каждое — по одному разу). Вася бросал все шесть кубиков шесть раз подряд. Ни на одном из кубиков не выпадало дважды одно и то же число. Известно, что при первом броске сумма чисел на верхних гранях равнялась 21, а при следующих четырёх бросках — 19, 20, 18 и 25. Какая сумма получилась при шестом броске?

