Задача 3.
Фишку поставили на некоторую клетку доски 5 × 5. Передвигая фишку на соседнюю по стороне клетку, обошли всю доску за исключением одной клетки и вернулись на стартовую позицию. В каждой клетке, кроме начальной, фишка побывала не более одного раза.
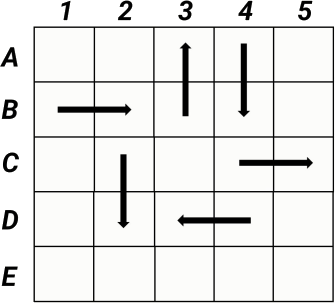
На рисунке изображены стрелочки, показывающие, куда передвигали фишку из некоторых клеток.
Выберите на картинке клетку, в которую фишка не заходила.
Ответ на Задачу 3.
Ответ: 𝐶1.
Решение:
Раз фишка вернулась в исходную клетку, будем считать её путь циклическим. Заметим, что никакая часть пути фишки не может рассекать доску на две области, в каждой из которых более 1 клетки, так как после прохождения этой части пути фишка должна перейти в одну из областей — а во вторую зайти уже не сможет, что противоречит условию.
Сначала установим, куда фишка могла пойти из клетки 𝐵2:
- в клетку 𝐴2 она перейти не могла, так как оттуда нельзя пройти ни в 𝐴1 (путь 𝐵1 → 𝐵2 → 𝐴2 → 𝐴1 не продолжается), ни в 𝐴3 (туда уже ведёт стрелка из другой клетки);
- в клетку 𝐵3 она перейти не могла, так как путь 𝐵1 → 𝐵2 → 𝐵3 → 𝐴3 рассекает доску на две области из более чем одной клетки.
Следовательно, из 𝐵2 фишка перешла в 𝐶2, а далее, согласно стрелке, в 𝐷2.
Куда фишка могла пойти из клетки 𝐷2?
- в 𝐷3 она перейти не могла, так как туда уже ведёт стрелка;
- в 𝐸2 она перейти не могла, так как путь 𝐵1 → 𝐵2 → 𝐶2 → 𝐷2 → 𝐸2 рассекает доску на две области из более чем одной клетки.
Следовательно, из 𝐷2 фишка перешла в 𝐷1. Ясно, что клетка 𝐶1 в таком случае должна остаться непосещённой, так как она отсечена частью пути 𝐵1 → 𝐵2 → 𝐶2 → 𝐷2 → 𝐷1.
Путь, удовлетворяющий условию и проходящий по всем остальным клеткам, приведён на рисунке ниже. Он строится единственным образом.


