Всероссийская олимпиада школьников по математике, 6 класс, 2022 год, 1 вариант
дата проведения: 19 октября 2022 - 21 октября 2022
источник: https://olympiads.mccme.ru/vmo/
Задача 6.
Женя покрасил три грани белого кубика 6 × 6 × 6 в красный цвет. Затем он распилил его на 216 одинаковых маленьких кубиков 1 × 1 × 1. Сколько у него могло получиться маленьких кубиков без красных граней? Укажите все возможные варианты.
Ответ на Задачу 6.
Ответ: 120, 125.
Решение:
Есть принципиально два случая раскраски граней большого кубика:
- три раскрашенные грани образуют «букву П»;
- три раскрашенные грани имеют общую вершину.
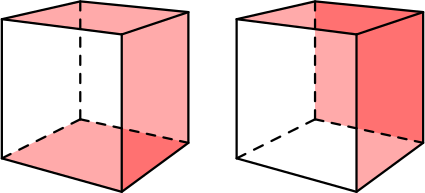
В первом случае, если «срезать» раскрашенные кубики 1 × 1 × 1, останется параллелепипед 4 × 5 × 6. Тогда маленьких кубиков без красных граней будет 4 ⋅ 5 ⋅ 6 = 120.
Во втором случае, если «срезать» раскрашенные кубики 1 × 1 × 1, останется кубик 5 × 5 × 5. Тогда маленьких кубиков без красных граней будет 5 ⋅ 5 ⋅ 5 = 125.
