Задача 6.
На плоскости отметили точки 𝐴, 𝐵, 𝐶, 𝐷, 𝐸 так, что треугольники 𝐴𝐵𝐶 и 𝐴𝐷𝐸 равны: 𝐴𝐵 = 𝐴𝐷, 𝐴𝐶 = 𝐴𝐸, 𝐵𝐶 = 𝐷𝐸. Затем с чертежа стёрли точку 𝐸 и подписи точек 𝐵, 𝐶 и 𝐷.
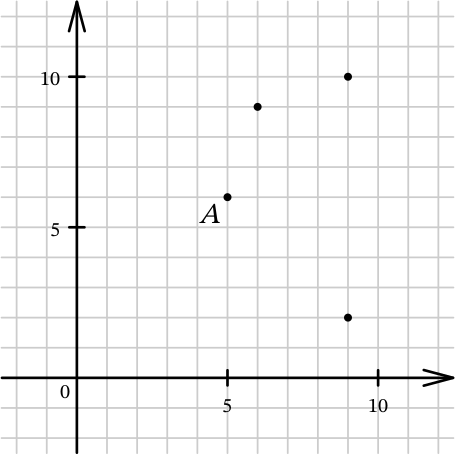
Пусть точка 𝐸 имела координаты (𝑥; 𝑦). Укажите все возможные значения величины 𝑥𝑦.
Ответ на Задачу 6.
Ответ: 14, 18, 40.
Решение:
Из условия 𝐴𝐵 = 𝐴𝐷 следует, что 𝐵 и 𝐷 — это две самые правые отмеченные точки (в неизвестном порядке). Оставшаяся неподписанная точка — это 𝐶.
Случай 1. Пусть точка 𝐵 находится сверху, а точка 𝐷 — снизу (первый рисунок ниже). Ясно, что для точки 𝐸 есть два варианта:
- точка 𝐸1 с координатами (8; 5);
- точка 𝐸2 с координатами (6; 3).

Случай 2. Пусть точка 𝐵 находится внизу, а точка 𝐷 — сверху. Ясно, что для точки 𝐸 есть два варианта:
- точка 𝐸3 с координатами (2; 7);
- точка 𝐸4 с координатами (6; 3).
Осталось лишь заметить, что точки 𝐸1 и 𝐸4 совпадают, поэтому есть ровно три возможных расположения точки 𝐸, а именно (2; 7), (6; 3) и (8; 5). Соответственно, произведение координат точки 𝐸 может принимать ровно три значения: 14, 18 и 40.

