Задача 1.
Внутри большого квадрата находится маленький квадрат, соответственные стороны этих квадратов параллельны. Расстояния между некоторыми сторонами квадратов отмечены на рисунке. На сколько периметр большого квадрата больше, чем периметр маленького?
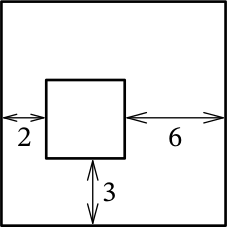
Задача 2.
Каждое из натуральных чисел 1, 2, 3, …, 377 покрашено либо в красный, либо в синий цвет (оба цвета присутствуют). Известно, что количество красных чисел равно наименьшему красному числу, а количество синих чисел равно наибольшему синему числу. Чему равно наименьшее красное число?
Задача 3.
Крош и Ёжик решили проверить, кто из них быстрее добежит по прямой дороге от домика Копатыча до домика Лосяша. Когда Крош пробежал 20 метров, Ёжик пробежал всего 16 метров. А когда Крошу оставалось 30 метров, Ёжику оставалось 60 метров. Сколько метров составляет длина дороги от домика Копатыча до домика Лосяша? (Крош и Ёжик выбежали одновременно, каждый из них бежал со своей постоянной скоростью.)
Задача 4.
Рассмотрим семизначные натуральные числа, в десятичной записи которых каждая из цифр 1, 2, 3, 4, 5, 6, 7 встречается ровно один раз.
- У скольких из них цифры с первой по шестую расположены в порядке возрастания, а с шестой по седьмую — в порядке убывания?
- У скольких из них цифры с первой по пятую расположены в порядке возрастания, а с пятой по седьмую — в порядке убывания?
Задача 5.
В лесу живут эльфы и гномы. Однажды 60 жителей этого леса встали в ряд лицом в одну сторону, в этот момент некоторые из них могли быть в колпаках. (Эльфов могло быть от 0 до 60 включительно, жителей в колпаках тоже могло быть от 0 до 60 включительно.) Каждый из 60 жителей сказал одну из следующих фраз:
- «Мой сосед справа — эльф».
- «Мой сосед справа — в колпаке».
Известно, что эльфы без колпаков всегда говорят правду, а эльфы в колпаках всегда лгут. У гномов всё наоборот: гномы без колпаков всегда лгут, а гномы в колпаках всегда говорят правду.
- Какое наибольшее количество эльфов без колпаков могло быть в ряду?
- Какое наибольшее количество эльфов в колпаках могло быть в ряду?
Задача 6.
На плоскости отметили точки 𝐴, 𝐵, 𝐶, 𝐷, 𝐸 так, что треугольники 𝐴𝐵𝐶 и 𝐴𝐷𝐸 равны: 𝐴𝐵 = 𝐴𝐷, 𝐴𝐶 = 𝐴𝐸, 𝐵𝐶 = 𝐷𝐸. Затем с чертежа стёрли точку 𝐸 и подписи точек 𝐵, 𝐶 и 𝐷.
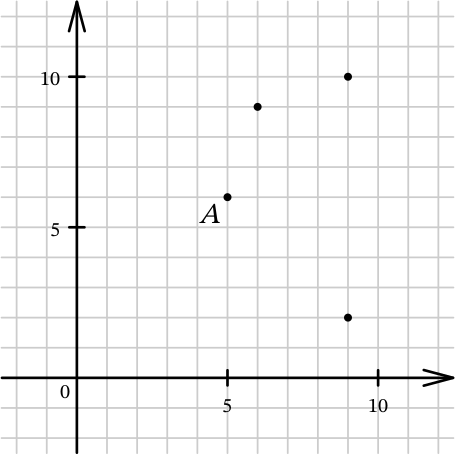
Пусть точка 𝐸 имела координаты (𝑥; 𝑦). Укажите все возможные значения величины 𝑥𝑦.
Задача 7.
На какое наибольшее количество групп можно разбить числа 1, 2, 3, …, 100 так, чтобы сумма чисел в каждой группе была простым числом? (Каждое число должно войти ровно в одну группу. Каждая группа должна состоять из одного или нескольких чисел.)
Задача 8.
Клетки таблицы 50 × 50 раскрашены в 𝑛 цветов так, что для любой клетки в объединении её строки и столбца встречаются клетки всех 𝑛 цветов. Найдите наибольшее возможное количество клеток синего цвета, если
- 𝑛 = 2;
- 𝑛 = 25.

