Задача 8.
Набор из 28 различных доминошек выглядит так:

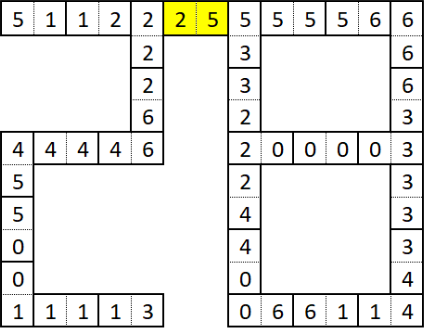
Все эти 28 доминошек выложили так, что количество точек на соприкасающихся половинках доминошек одинаково. На некоторых половинках полностью стёрли количество точек. В итоге получилась конструкция, изображённая на рисунке ниже (пустые половинки могли быть изначально пустыми, а могли содержать какое-то количество точек).
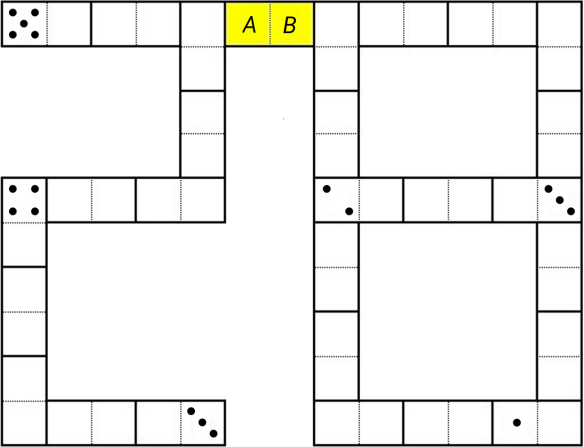
Сколько точек на каждой из половинок жёлтой костяшки (на половинке 𝐴 и на половинке 𝐵)?
Ответ на Задачу 8.
Ответ: 𝐴 = 2, 𝐵 = 5.
Решение:
Сначала заметим, что любое число должно встречаться ровно на 8 половинках доминошек (на 6 доминошках в паре с другими числами и на одной доминошке дважды). То есть каждое число встречается чётное количество раз.
Рассмотрим выделенные красные области из 1 или 3 клеток. По условию числа на соприкасающихся половинках равны, а значит, внутри каждой выделенной области стоят одинаковые числа. Все остальные половинки доминошек разбиваются на пары соседних, где также должны стоять одинаковые числа.
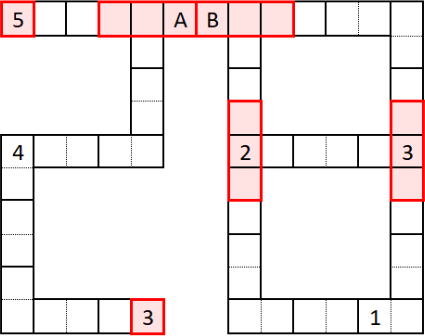
Получаем, что вне выделенных областей каждое число встречается чётное число раз. Значит, чтобы число встречалось чётное число раз во всей раскладке доминошек, количество выделенных красных областей с каждым числом должно быть чётно. Мы знаем, что стоит во всех выделенных областях, кроме областей с половинками 𝐴 и 𝐵. Теперь заметим, что только числа 2 и 5 присутствуют в нечётном количестве (в одной выделенной области), а значит, в областях с половинками 𝐴 и 𝐵, должны стоять именно они.
Осталось понять, где именно стоит 2, а где 5. Предположим, что в половинке 𝐴 стоит 5, тогда все половинки левее данной определяются однозначно, и две выделенные на картинке доминошки получаются одинаковыми, чего быть не может.
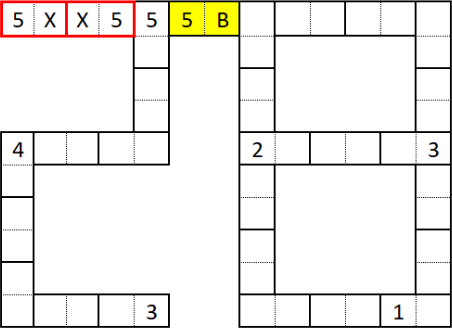
Получаем, что единственный возможный вариант — это 𝐴 = 2 и 𝐵 = 5.
Замечание: Одна из возможных конфигураций доминошек изображена на рисунке ниже.