Решите ребус:

𝐶,𝐵𝐴 + 𝐴,𝐴𝐴 = 𝐵,𝐴.

Разными буквами обозначены разные цифры, одинаковыми буквами — одинаковые цифры. Запятая — это десятичный знак.

Влад и Дима решили подзаработать. Каждый из них решил положить по 3000 рублей в банк, а через год все деньги снять.

• Влад выбрал вклад «Уверенность»: за год сумма увеличивается на 20%, но при снятии банк взимает комиссию 10%.
• Дима выбрал вклад «Надёжность»: за год сумма увеличивается на 40%, но при снятии банк взимает комиссию 20%.

(«Банк взимает комиссию 𝑛%» означает то, что банк оставляет себе 𝑛% от текущей величины вклада, а оставшуюся часть вклада возвращает его владельцу.)

Кто получит большую годовую прибыль от вклада? Чему будет равна разница? Ответ выразите в рублях.

Смешарики Крош, Ёжик, Нюша и Бараш суммарно съели 86 конфет, причём каждый из них съел не менее 5 конфет. Известно, что:

• Нюша съела конфет больше, чем каждый из остальных смешариков;
• Крош и Ёжик суммарно съели 53 конфеты.

Сколько конфет съела Нюша?

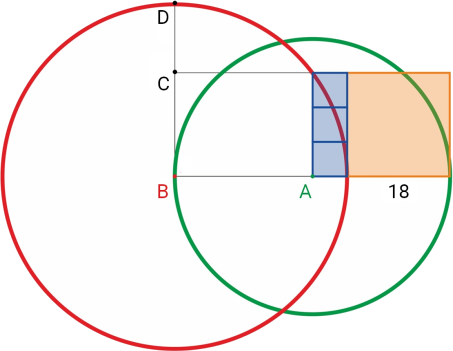
На рисунке ниже:

• три синие фигуры — квадраты;
• оранжевая фигура — квадрат со стороной 18;
• точка 𝐴 — центр зелёной окружности;
• точка 𝐵 — центр красной окружности.

Найдите длину отрезка 𝐶𝐷.

В магазине продаются орехи четырёх видов: фундук, миндаль, кешью и фисташки. Степан хочет купить 1 килограмм орехов одного вида и ещё 1 килограмм орехов — другого. Он вычислил, во сколько ему может обойтись такая покупка в зависимости от того, какие два вида орехов он выберет. Пять из шести возможных покупок Степана стоили бы 1900, 2070, 2110, 2330 и 2500 рублей. Сколько рублей составляет стоимость шестой возможной покупки?

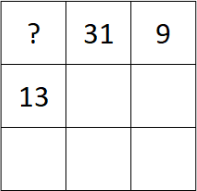
Магический квадрат — это таблица 3 × 3, в которой расставлены числа так, что суммы по всем строкам, столбцам и двум главным диагоналям одинаковы. На рисунке изображён магический квадрат, в котором все числа, кроме трёх, стёрты. Найдите, чему равно число в левом верхнем углу квадрата.

Все 25 учеников 7 «А» класса участвовали в викторине из трёх туров. В каждом туре каждый участник набрал некоторое количество очков. Известно, что в каждом туре, а также по сумме всех трёх туров все участники набрали различное количество очков.

Ученик 7 «А» Коля в первом туре викторины оказался третьим, во втором — четвёртым, а в третьем — пятым. Какое самое низкое место мог занять Коля среди всех одноклассников по сумме очков за все три тура викторины?

Набор из 28 различных доминошек выглядит так:

Все эти 28 доминошек выложили так, что количество точек на соприкасающихся половинках доминошек одинаково. На некоторых половинках полностью стёрли количество точек. В итоге получилась конструкция, изображённая на рисунке ниже (пустые половинки могли быть изначально пустыми, а могли содержать какое-то количество точек).

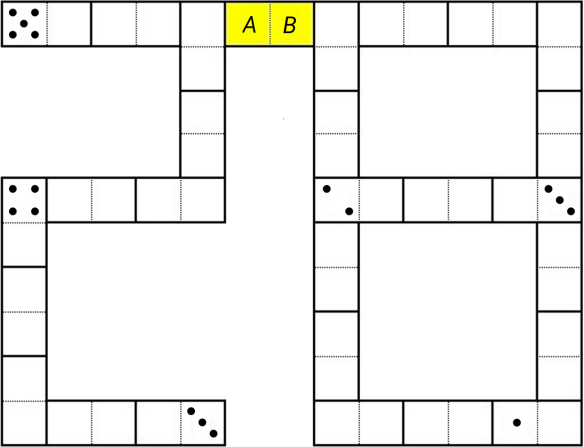
Сколько точек на каждой из половинок жёлтой костяшки (на половинке 𝐴 и на половинке 𝐵)?