Задача 5.
В выпуклом четырёхугольнике $ABCD$ биссектрисы углов $A$ и $C$ параллельны, а биссектрисы углов $B$ и $D$ пересекаются под углом 46°, как изображено на рисунке. Сколько градусов составляет острый угол между биссектрисами углов $A$ и $B$?
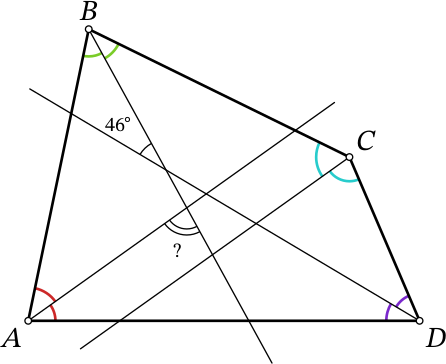
Ответ на Задачу 5.
Ответ: 67°.
Решение:
Отметим точки пересечения биссектрис $K$, $L$, $M$, $N$ (см. рисунок ниже).
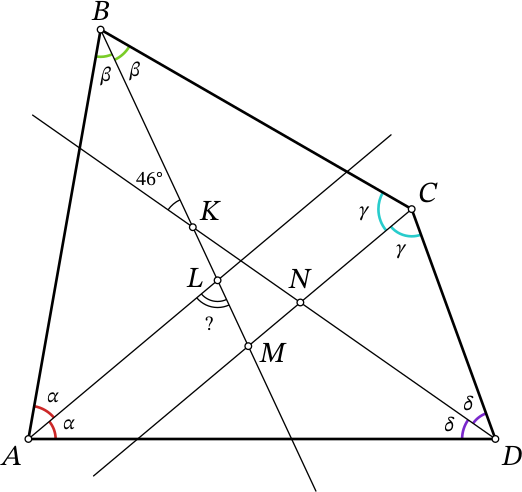
Кроме этого, обозначим $\angle A$ = $2\alpha$, $\angle B$ = $2\beta$, $\angle C$ = $2\gamma$, $\angle D$ = $2\delta$. Поскольку сумма углов четырёхугольника $ABCD$ равна 360°, имеем:
$ 2\alpha + 2\beta + 2\gamma + 2\delta = 360°$
$ \alpha + \beta + \gamma + \delta = 180°$
Рассмотрим треугольник $KMN$. В нём:
- $\angle MKN$ = $46°$,
- $\angle KMN$ = $\angle ALM$ = $\alpha + \beta$, так как $ALM$ — внешний угол треугольника $ABL$ (этот угол и нужно найти в задаче),
- $\angle KNM$ = $\angle CND$ = $180° − \gamma − \delta = \alpha + \beta$.
Следовательно, треугольник $KMN$ — равнобедренный, и $\angle KMN$ = $\displaystyle \frac{180° − 46°}{2}$ = 67°.
Другое решение:
Зафиксируем угол $A$ и перенесём параллельно угол $C$ так, чтобы вершина $C$ оказалась на биссектрисе угла $A$. (Или более формально, отметим на биссектрисе угла $A$ точку $C'$ и проведём из неё лучи, сонаправленные лучам $CB$ и $CD$; пересечения этих лучей с лучами $AB$ и $AD$ соответственно обозначим через $B'$ и $D'$, как на рисунке ниже)
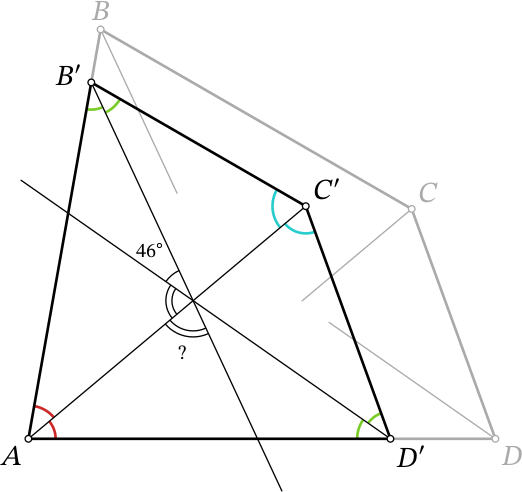
Стороны нового четырёхугольника $AB'C'D'$ параллельны сторонам исходного; значит, и углы между этими сторонами такие же. Следовательно, биссектрисы нового четырёхугольника параллельны соответствующим биссектрисам исходного, и углы между ними тоже сохранились.
Но это означает, что биссектрисы углов $A$ и $C'$ совпадают, то есть вся новая картинка симметрична относительно прямой $AC^{\prime}$ (из равенства треугольников $AB'C'$ и $AD'C'$ по общей стороне и прилежащим к ней углам). Из симметрии следует, что другие две биссектрисы пересекаются на прямой $AC'$ и образуют с ней равные углы. Тогда искомый угол после удвоения будет дополнять 46° до развёрнутого. Следовательно, он равен $\frac{1}{2}\left(180° − 46°\right)$ = 67°.

