Задача 1.
В ящике лежат апельсины, груши и яблоки, всего 60 фруктов. Известно, что яблок в 3 раза больше, чем не яблок, а груш в 5 раз меньше, чем не груш. Сколько апельсинов лежит в ящике?
Задача 2.
Олег купил шоколадку за 𝑛 рублей, а через некоторое время продал её за 96 рублей. Оказалось, что он продал шоколадку ровно на 𝑛% дороже, чем покупал. За сколько рублей Олег купил шоколадку?
Задача 3.
У Маши есть три одинаковых игральных кубика, на гранях каждого из них написано шесть различных простых чисел с суммой 87. Маша дважды кинула все три кубика. В первый раз сумма выпавших чисел равнялась 10, во второй раз сумма выпавших равнялась 62.
Ровно одно из шести чисел ни разу не выпало. Какое?
Задача 4.
В клетках таблицы 2 × 35 (2 строки, 35 столбцов) расставлены ненулевые действительные числа, причём в верхней строке все числа различны. Для любых двух чисел, стоящих в одном столбце, выполнено следующее условие: одно число является квадратом другого.
- Какое наибольшее количество отрицательных чисел может быть в этой таблице?
- Какое наименьшее количество различных чисел может быть в нижней строке?
Задача 5.
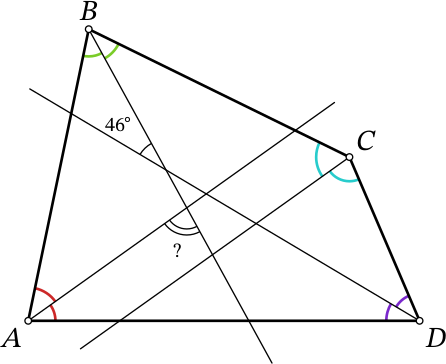
В выпуклом четырёхугольнике $ABCD$ биссектрисы углов $A$ и $C$ параллельны, а биссектрисы углов $B$ и $D$ пересекаются под углом 46°, как изображено на рисунке. Сколько градусов составляет острый угол между биссектрисами углов $A$ и $B$?
Задача 6.
Натуральное число 𝑛 таково, что значение выражения 𝑛2 + 492 является точным квадратом. Чему может быть равно 𝑛? Укажите все возможные варианты.
Задача 7.
Сколько существует способов расположить в ряд 𝑛 крестиков и 13 ноликов так, чтобы среди любых трёх подряд идущих значков нашёлся хотя бы один нолик, если
- 𝑛 = 27
- 𝑛 = 26
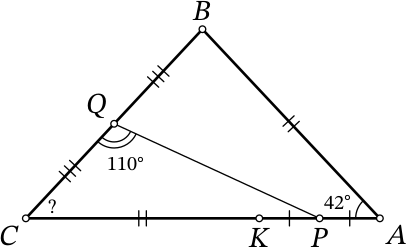
Задача 8.
Дан треугольник $ABC$, в котором $\angle A$ = 42° и $AB<AC$. Точка $K$ на стороне $AC$ такова, что $AB = CK$. Точки $P$ и $Q$ — середины отрезков $AK$ и $BC$ соответственно. Сколько градусов составляет угол $ACB$, если известно, что $\angle PQC$ = 110°?