Задача 8.
Дан треугольник $ABC$, в котором $\angle A$ = 42° и $AB<AC$. Точка $K$ на стороне $AC$ такова, что $AB = CK$. Точки $P$ и $Q$ — середины отрезков $AK$ и $BC$ соответственно. Сколько градусов составляет угол $ACB$, если известно, что $\angle PQC$ = 110°?
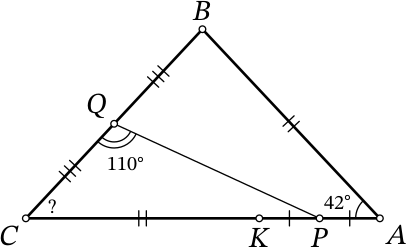
Ответ на Задачу 8.
Ответ: 49°.
Решение:
Отметим на продолжении стороны $CA$ за точку $A$ точку $L$ такую, что $AL = AB$ (см. рисунок).
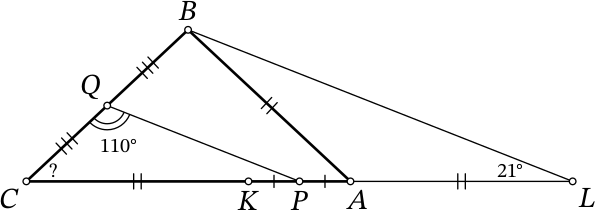
Заметим, что прямая $PQ$ параллельна прямой $BL$ как средняя линия в треугольнике $BCL$. Получаем, что $\angle LBC$ = $\angle PQC$ = 110°.
В равнобедренном треугольнике $BAL$ внешний угол при вершине $A$ равен 42°, поэтому углы при основании равны $\angle ALB$ = $\angle ABL$ = $\frac{1}{2}⋅42° = 21°$.
Из суммы углов треугольника $BCL$ находим искомый угол:
$ \angle ACB$ = $180° − \angle CLB − \angle LBC$ = 180° − 110° − 21° = 49°.

