Всероссийская олимпиада школьников по математике, 8 класс, 2022 год, 2 этап
дата проведения: 19 октября 2022 - 21 октября 2022
источник: https://olympiads.mccme.ru/vmo/
Задача 7.
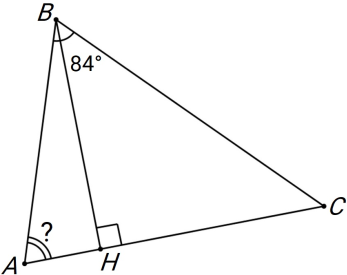
В остроугольном треугольнике 𝐴𝐵𝐶 проведена высота 𝐵𝐻. Оказалось, что 𝐶𝐻 = 𝐴𝐵 + 𝐴𝐻. Сколько градусов составляет угол 𝐵𝐴𝐶, если ∠𝐴𝐵𝐶 = 84°?
Ответ на Задачу 7.
Ответ: 64°.
Решение:
Отметим на отрезке 𝐶𝐻 точку 𝐾 такую, что 𝐴𝐻 = 𝐻𝐾. Тогда из условия следует, что 𝐴𝐵 = 𝐶𝐾 (см. рисунок).
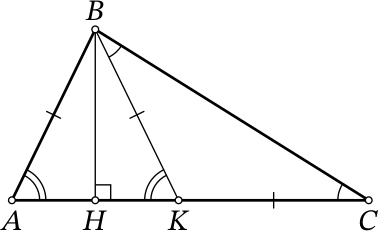
В треугольнике 𝐴𝐵𝐾 высота 𝐵𝐻 совпадает с медианой, поэтому он является равнобедренным, 𝐴𝐵 = 𝐵𝐾 и ∠𝐵𝐴𝐻 = ∠𝐵𝐾𝐴.
Пусть ∠𝐴𝐶𝐵 = 𝑥. Поскольку 𝐶𝐾 = 𝐴𝐵 = 𝐵𝐾, треугольник 𝐵𝐶𝐾 является равнобедренным, и ∠𝐾𝐵𝐶 = ∠𝐾𝐶𝐵 = 𝑥. Тогда ∠𝐴𝐾𝐵 = 2𝑥, ∠𝐾𝐴𝐵 = 2𝑥 и ∠𝐴𝐵𝐶 = 180° − 3𝑥.
Поскольку 84° = ∠𝐴𝐵𝐶 = 180° −3𝑥, находим 𝑥 = 32°. Тем самым, ∠𝐵𝐴𝐶 = 2⋅32° = 64°.
