Задача 1.
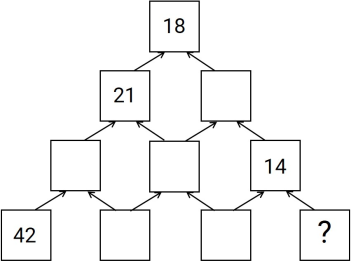
Клетки пирамиды заполнили по следующему правилу: над каждыми двумя соседними числами записали их среднее арифметическое. Некоторые числа стёрли, и получилась конструкция, изображённая на рисунке. Какое число было в правой нижней клетке? (Среднее арифметическое двух чисел — это их сумма, разделённая на 2.)
Задача 2.
Малыши Коля и Маша учатся считать. В первую секунду Коля назвал число 1, во вторую — 2, в третью — 3 и т. д. Если Маше нравится число, названное Колей, то она записывает его себе в тетрадь, в конец текущей строки (одно число за другим, без пробелов и запятых). Спустя 𝑛 секунд у Маши в тетради оказалось записано:
2 7 2 6 2 5 2 4 2 3
Какое наименьшее значение может принимать 𝑛?
Задача 3.
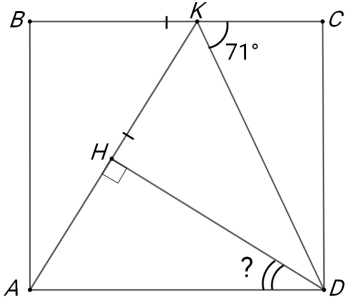
На стороне 𝐵𝐶 прямоугольника 𝐴𝐵𝐶𝐷 отмечена точка 𝐾. Точка 𝐻 на отрезке 𝐴𝐾 такова, что ∠𝐴𝐻𝐷 = 90°. Оказалось, что 𝐴𝐾 = 𝐵𝐶. Сколько градусов составляет угол 𝐴𝐷𝐻, если ∠𝐶𝐾𝐷 = 71°?
Задача 4.
По кругу стоят 36 детей, каждый из них одет в красную или синюю кофту. Известно, что рядом с каждым мальчиком стоит девочка, а рядом с каждой девочкой стоит человек в синей кофте. Найдите наибольшее возможное количество девочек в красных кофтах.
Задача 5.
Из города в деревню выехал автомобиль, одновременно с ним из деревни в город выехал велосипедист. Когда автомобиль и велосипедист встретились, автомобиль сразу же развернулся и поехал обратно в город. В итоге велосипедист приехал в город на 35 минут позже автомобиля. Сколько минут затратил велосипедист на весь путь, если известно, что его скорость в 4,5 раза меньше скорости автомобиля?
Задача 6.
Паша выписал в порядке возрастания все натуральные делители натурального числа 𝑘 и их пронумеровал: первый, второй, ….
Паша заметил, что если шестой делитель умножить на тринадцатый делитель, то получится исходное число 𝑘.
Сколько натуральных делителей имеет число 𝑘?
Задача 7.
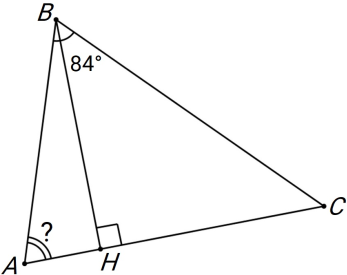
В остроугольном треугольнике 𝐴𝐵𝐶 проведена высота 𝐵𝐻. Оказалось, что 𝐶𝐻 = 𝐴𝐵 + 𝐴𝐻. Сколько градусов составляет угол 𝐵𝐴𝐶, если ∠𝐴𝐵𝐶 = 84°?
Задача 8.
На острове живут рыцари, которые всегда говорят правду, и лжецы, которые всегда лгут.
Однажды собрались 10 жителей острова, все они надели на себя футболки с номерами от 1 до 10 (у разных жителей разные номера). Каждый из них сказал одну из фраз:
- «Среди собравшихся нет рыцаря, номер футболки которого больше моего»
- «Среди собравшихся нет лжеца, номер футболки которого меньше моего».
Известно, что каждая из этих фраз прозвучала ровно 5 раз. Сколько рыцарей могло быть среди этих 10 жителей? Укажите все возможные варианты.

