Всероссийская олимпиада школьников по математике, 9 класс, 2022 год
дата проведения: 19 октября 2022 - 21 октября 2022
источник: https://olympiads.mccme.ru/vmo/
Задача 6.
Дан тупоугольный треугольник 𝐴𝐵𝐶 с тупым углом 𝐶. На его сторонах 𝐴𝐵 и 𝐵𝐶 отмечены точки 𝑃 и 𝑄 соответственно так, что ∠𝐴𝐶𝑃 = 𝐶𝑃𝑄 = 90°. Найдите длину отрезка 𝑃𝑄, если известно, что 𝐴𝐶 = 25, 𝐶𝑃 = 20, ∠𝐴𝑃𝐶 = ∠𝐴 + ∠𝐵.
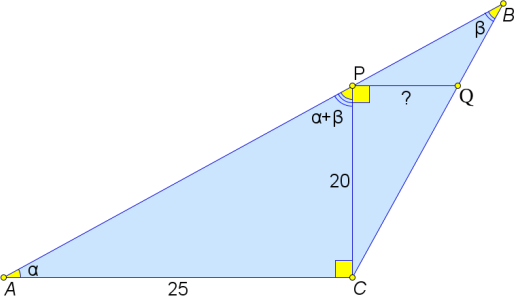
Ответ на Задачу 6.
Ответ: 16.
Решение:
Поскольку ∠𝑃𝐶𝐵 + ∠𝑃𝐵𝐶 = ∠𝐴𝑃𝐶 = ∠𝑃𝐴𝐶 + ∠𝑃𝐵𝐶, получаем ∠𝑃𝐶𝐵 = ∠𝑃𝐴𝐶. Заметим, что прямоугольные треугольники 𝑃𝐴𝐶 и 𝑄𝐶𝑃 подобны по острому углу, и
$$ \frac{25}{20}=\frac{A C}{C P}=\frac{P C}{P Q}=\frac{20}{P Q} $$
откуда находим 𝑃𝑄 = 20 ⋅ 20 / 25 = 16.
