Задача 1.
В магазине продаётся 20 товаров, стоимости которых — различные натуральные числа от 1 до 20 рублей. Магазин решил устроить акцию: при покупке любых 5 товаров один из них выдаётся в подарок, причём покупатель сам выбирает, какой товар получит бесплатно. Влад хочет купить все 20 товаров в этом магазине, заплатив как можно меньше. Сколько рублей ему понадобится? (Каждый из 20 товаров продаётся в 1 экземпляре.)
Задача 2.
Ваня загадал два натуральных числа, произведение которых равняется 7200. Какое наибольшее значение может принимать НОД этих чисел?
Задача 3.
Четыре города и пять дорог расположены так, как изображено на рисунке. Длины всех дорог равны целому числу километров. Длины четырёх дорог указаны на рисунке. Сколько километров составляет длина оставшейся?
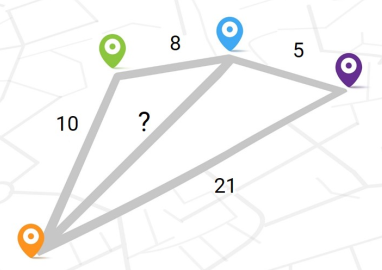
Задача 4.
Простое число 𝑝 таково, что число 𝑝 + 25 является седьмой степенью простого числа. Чему может быть равно 𝑝? Укажите все возможные варианты.
Задача 5.
На острове живут рыцари, которые всегда говорят правду, и лжецы, которые всегда лгут.
Однажды собрались 80 жителей острова, все они надели на себя футболки с номерами от 1 до 80 (у разных жителей разные номера). Каждый из них сказал одну из двух фраз:
- «Среди собравшихся хотя бы у 5 лжецов номер футболки больше моего».
- «Среди собравшихся хотя бы у 5 лжецов номер футболки меньше моего».
Какое наименьшее количество рыцарей могло быть среди этих 80 жителей?
Задача 6.
Дан тупоугольный треугольник 𝐴𝐵𝐶 с тупым углом 𝐶. На его сторонах 𝐴𝐵 и 𝐵𝐶 отмечены точки 𝑃 и 𝑄 соответственно так, что ∠𝐴𝐶𝑃 = 𝐶𝑃𝑄 = 90°. Найдите длину отрезка 𝑃𝑄, если известно, что 𝐴𝐶 = 25, 𝐶𝑃 = 20, ∠𝐴𝑃𝐶 = ∠𝐴 + ∠𝐵.
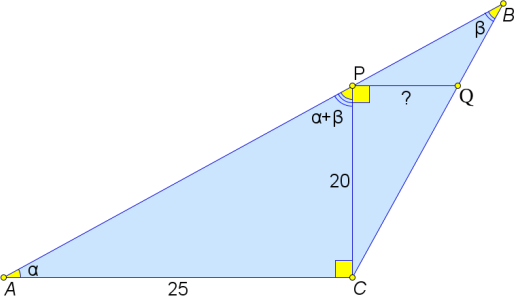
Задача 7.
Дан квадратный трёхчлен 𝑃(𝑥), старший коэффициент которого равен 1. На графике 𝑦 = 𝑃(𝑥) отметили две точки с абсциссами 10 и 30. Оказалось, что биссектриса первой четверти координатной плоскости пересекает отрезок между ними в его середине. Найдите 𝑃(20).
Задача 8.
В таблице 8 × 12 некоторые 𝑁 клеток — чёрные, а остальные — белые. За одну операцию разрешается покрасить три клетки, образующие трёхклеточный уголок, в белый цвет (некоторые из них ещё до перекрашивания могли быть белыми). Оказалось, что таблицу невозможно сделать полностью белой менее чем за 25 таких операций. Найдите наименьшее возможное значение 𝑁.

