Задача 8.
В таблице 8 × 12 некоторые 𝑁 клеток — чёрные, а остальные — белые. За одну операцию разрешается покрасить три клетки, образующие трёхклеточный уголок, в белый цвет (некоторые из них ещё до перекрашивания могли быть белыми). Оказалось, что таблицу невозможно сделать полностью белой менее чем за 25 таких операций. Найдите наименьшее возможное значение 𝑁.
Ответ на Задачу 8.
Ответ: 27.
Решение:
Разобьём таблицу 8 × 12 на 24 квадрата 2 × 2 (см. первый рисунок):
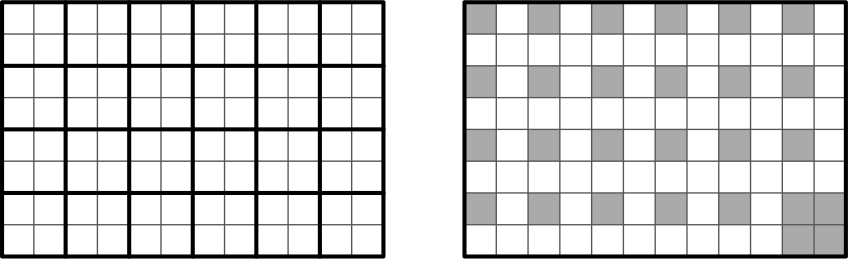
Сначала покажем, как можно покрасить в чёрный цвет 27 клеток требуемым образом. В каждом квадрате 2 × 2 покрасим верхнюю левую клетку, а в правом нижнем квадрате также закрасим все остальные клетки (см. второй рисунок). Заметим, что никакой трёхклеточный уголок не может одновременно накрыть чёрные клетки из двух разных квадратов 2 × 2. Поэтому потребуется не менее 2 операций для правого нижнего квадрата, и ещё 23 операции для оставшихся квадратов, т. е. суммарно не менее 25 операций.
Теперь покажем, что если чёрных клеток 26, то таблицу можно гарантированно сделать полностью белой не более чем за 24 операции (если изначально чёрных клеток меньше 26, то некоторые белые можно считать чёрными). Для этого нам достаточно либо один раз перекрасить 3 чёрные клетки в белый цвет, либо дважды перекрасить 2 чёрные клетки в белый цвет. Действительно, после таких действий количество доступных операций будет не меньше оставшегося количества чёрных клеток, поэтому дальше достаточно будет каждый раз перекрашивать хотя бы по одной чёрной клетке.
Поскольку чёрных клеток всего 26, а квадратов 2 × 2 всего 24, то как раз либо в каком-то квадрате есть 3 чёрные клетки, либо хотя бы в двух квадратах есть по 2 чёрные клетки (иначе чёрных клеток не больше 24 + 1 = 25). Перекрасив соответствующие трёхклеточные уголки, а затем перекрашивая хотя бы по одной чёрной клетке, добьёмся требуемого не более чем за 24 операции.

