Задача 6.
На рисунке изображён прямоугольник, разрезанный на семь квадратов.
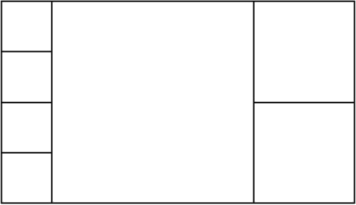
Найдите периметр этого прямоугольника, если его площадь равна 2268.
Ответ на Задачу 6.
Ответ: 198.
Решение:
Заметим, что сторона большого квадрата в 4 раза больше стороны маленького квадрата, поэтому большой квадрат можно разрезать на 16 маленьких квадратов.
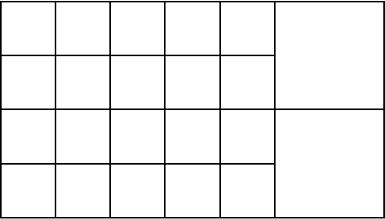
Теперь видно, что сторона среднего квадрата в 2 раза больше стороны маленького квадрата, поэтому каждый из средних квадратов можно разрезать на 4 маленьких квадрата.
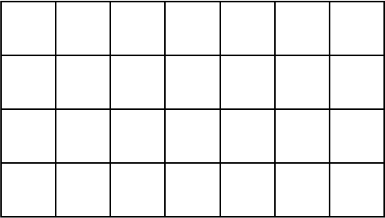
Пусть 𝑥 — площадь маленького квадрата. Тогда площадь всего прямоугольника равна 28𝑥, а по условию задачи она равна 2268. Получается уравнение:
28𝑥 = 2268,
𝑥 = 81.
Отсюда можно понять, что маленький квадрат имеет размеры 9 × 9.
Периметр всего прямоугольника равен 2⋅(4𝑥 + 7𝑥) = 22𝑥, и он в 22 раза больше стороны маленького квадрата. Значит, ответом к задаче является число 22 ⋅ 9 = 198.

