Задача 7.
У Вани есть 234 монеты и доска 7 × 7. Он разложил все монеты в клетки доски так, что в любых четырёх клетках, образующих прямоугольник 1 × 4 или 4 × 1, суммарно оказалось ровно 19 монет (в каких-то клетках могло оказаться несколько монет, а какие-то клетки могли оказаться пустыми).
Сколько всего монет может находиться в четвёртом столбце? Укажите все возможные варианты.
Ответ на Задачу 7.
Ответ: 32 монеты.
Решение:
Разобьём наш квадрат на 12 прямоугольников 1 × 4 и 1 квадратик 1 × 1, как показано на рисунке (a).
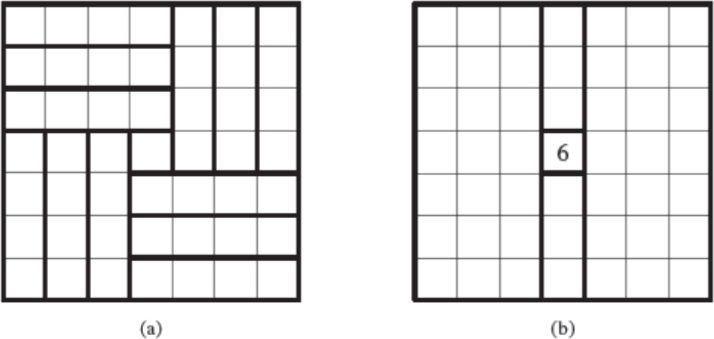
Из условия задачи следует, что суммарное количество монет во всех 12 прямоугольниках равно 12 ⋅ 19 = 228. Поскольку всего монет 234, то в центральном квадратике 1 × 1 лежат ровно 234 − 228 = 6 монет.
Теперь рассмотрим два прямоугольника 1 × 4 в четвёртом столбце: образованный верхними 4 клетками и образованный нижними 4 клетками (рисунок (b)). Чтобы найти количество монет в четвёртом столбце, мы сложим количества монет в этих двух прямоугольниках:
19 + 19 = 38 монет. Но при этом монеты в центральном квадратике посчитаны дважды, поэтому их количество надо вычесть: 38 − 6 = 32 монеты.

