Задача 7.
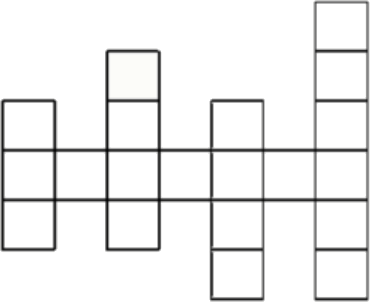
На рисунке изображена клетчатая доска. Будем считать, что фишка на этой доске видит другую фишку, если они расположены либо в одной вертикали, либо в одной горизонтали, причём между ними нет границ доски. Сколькими способами можно расставить 5 фишек на этой доске так, чтобы никакие две из них не видели друг друга?
Ответ на Задачу 7.
Ответ: 270 вариантов.
Решение:
Доска состоит из пяти пересекающихся элементов — четыре вертикали и одна горизонталь. Фишек тоже пять, поэтому на одном элементе (вертикали или горизонтали) можно поставить только одну фишку.
Клетки, находящиеся на пересечении вертикалей и горизонталей не могут участвовать в размещении, т.к. тогда фишки на разных элементах увидят друг друга.
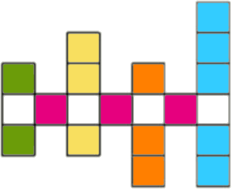
Цветом обозначим варианты размещения каждой фишки в пределах своего элемента. Подсчитаем количество клеток на каждом элементе, на которые можно ставить фишки:
- Первая вертикаль — 2 клетки
- Вторая вертикаль — 3 клетки
- Третья вертикаль — 3 клетки
- Четвёртая вертикаль — 5 клеток
- Горизонталь — 3 клетки
Количество вариантов размещения пяти фишек равно произведению вариантов для каждой отдельной фишки:
N = 2 ⋅ 3 ⋅ 3 ⋅ 5 ⋅ 3 = 270 вариантов.

