Задача 4.
В 10 кружков на картинке расставили целые числа от 1 до 10, каждое по разу. Между некоторыми парами из них нарисовали стрелку или отрезок, руководствуясь следующими правилами:
- Если одно число делится на другое, то от большего числа нарисовали стрелку к меньшему;
- Если ни одно число не делится на другое, то между ними нарисовали отрезок.
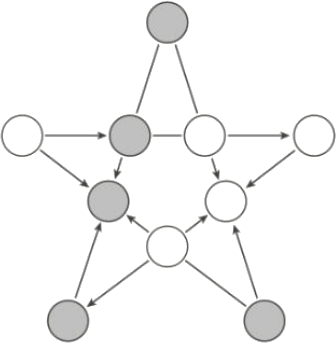
Затем все исходные числа стёрли. Восстановите, где какое число стояло. В ответ запишите в произвольном порядке 5 чисел, которые стояли в пяти серых кружках.
Ответ на Задачу 4.
Ответ: 1, 3, 5, 6, 7.
Решение:
Обозначим числа, стоящие в кружках, латинскими буквами от 𝐴 до 𝐽, как на рисунке (a):
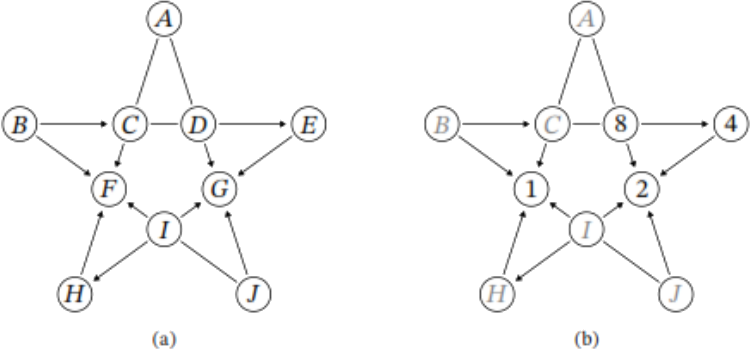
Заметим, что каждому из чисел 𝐹 и 𝐺 кратны по четыре других числа. Среди чисел от 1 до 10 только 1 или 2 обладают таким свойством, поэтому 𝐹 и 𝐺 — это числа 1 и 2 в некотором порядке.
Предположим, что 𝐹 = 2, тогда 𝐵, 𝐶, 𝐻, 𝐼 — это остальные чётные числа 4, 6, 8, 10 в некотором порядке. Заметим, что 𝐵 должно делиться на 𝐶, а 𝐼 должно делиться на 𝐻. Но среди чисел 4, 6, 8, 10 только одна пара кратных друг другу: 8 и 4; поэтому такая ситуация невозможна, и 𝐺 = 2, а 𝐹 = 1. Сразу отметим, что по аналогичным соображениям в соседних с числом 2 кружках стоят числа 4, 6, 8, 10, причём 𝐷 = 8, а 𝐸 = 4, так как они соединены стрелкой (рисунок. (b)).
Теперь рассмотрим число 𝐼, оно равно 6 или 10. Предположим, что 𝐼 = 6, тогда 𝐽 = 10. Получаем, что 6 должно делиться на 𝐻, а из ещё не расставленных чисел под это условие подходит только число 3. Остались числа 5, 7 и 9; ни одно из них не делится на другое, но 𝐵 должно делиться на 𝐶. Противоречие. Значит, данный случай невозможен; тогда 𝐼 = 10, а 𝐽 = 6 (рисунок. (a) ниже).
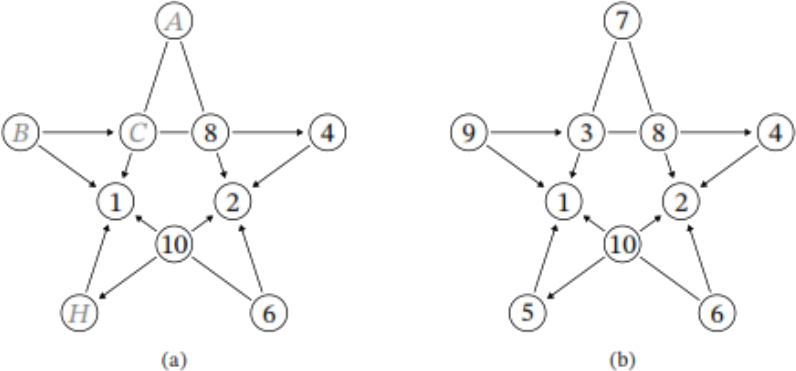
Далее заметим, что 10 должно делиться на 𝐻 — из ещё не расставленных чисел под это условие подходит только число 5. Остались числа 3, 7, 9, среди них только 9 делится на 3, а значит, 𝐵 = 9, 𝐶 = 3 и 𝐴 = 7.
Получаем, что существует единственная расстановка чисел от 1 до 10, удовлетворяющая условию задачи. Следовательно, числа в выделенных кружках — это 1, 3, 5, 6, 7.

