Задача 1.
Гоша нашёл в кабинете естествознания 3 гири и весы. После того как он всё взвесил, оказалось, что:
- Первая гиря в 4 раза тяжелее второй;
- Третья гиря в 3 раза тяжелее первой;
- Суммарный вес всех гирь — 340 грамм.
Определите вес первой гири. Ответ выразите в граммах.
Задача 2.
В 7«А» учится 26 детей, которые на всех уроках сидят по двое за партой. Однажды в этом классе провели самостоятельную работу, за которую каждый получил четвёрку или пятёрку.
Все ученики заявили следующее: «Все сидящие не за одной партой со мной получили четвёрки.»
Оказалось, что правду сказали только те ученики, которые получили пятёрку. Сколько всего четвёрок было выставлено за эту самостоятельную работу?
Задача 3.
У сладкоежек Пети и Васи были конфеты, у каждого более 1000 конфет. Известно, что у Пети конфет было на 324 больше, чем у Васи. Каждый день они одновременно обменивались конфетами: Петя отдавал треть своих конфет Васе, а Вася отдавал треть своих конфет Пете. У кого из них через 3 дня оказалось больше конфет?
Задача 4.
В 10 кружков на картинке расставили целые числа от 1 до 10, каждое по разу. Между некоторыми парами из них нарисовали стрелку или отрезок, руководствуясь следующими правилами:
- Если одно число делится на другое, то от большего числа нарисовали стрелку к меньшему;
- Если ни одно число не делится на другое, то между ними нарисовали отрезок.
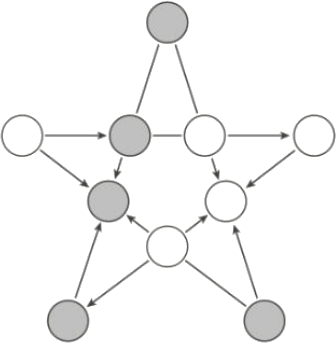
Затем все исходные числа стёрли. Восстановите, где какое число стояло. В ответ запишите в произвольном порядке 5 чисел, которые стояли в пяти серых кружках.
Задача 5.
По кругу стоят 36 натуральных чисел (не обязательно различных). Известно, что в каждой тройке подряд идущих чисел есть число, большее суммы двух других. Какое наименьшее значение может принимать сумма всех 36 чисел?
Задача 6.
На рисунке изображены прямоугольники с одинаковыми периметрами: синие и красные, причём одноцветные прямоугольники равны друг другу. Два отмеченных отрезка равны 8 и 4 соответственно. Найдите длину отрезка, обозначенного знаком «?».
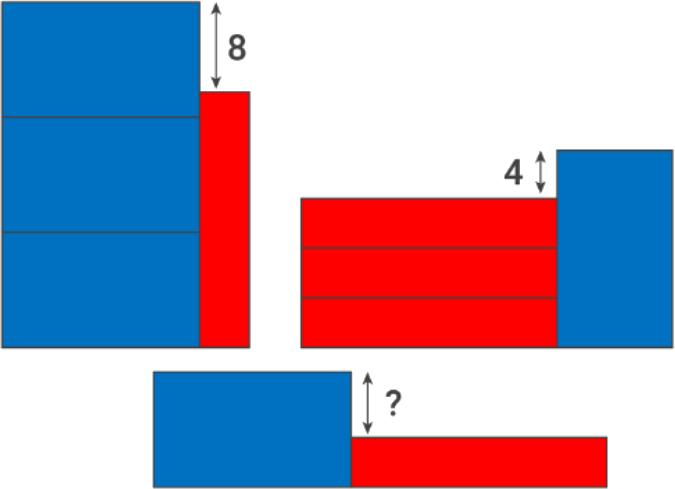
Задача 7.
На доске в строчку выписаны семь красных целых чисел, среднее арифметическое которых равно 18. Паша собирается записать под каждым красным числом синее целое число, отличающееся от него не более чем на 3 (возможно, равное красному). Сколько различных значений (не обязательно целых) может принимать среднее арифметическое семи синих чисел?
Задача 8.
У Коли есть 100 монет и доска 𝑚 × 𝑛, где 𝑚 ≥ 𝑛 и 𝑚 > 1. Он разложил все монеты в клетки доски так, что в любых двух соседних по стороне клетках суммарно оказалось ровно 10 монет (в каких-то клетках могло оказаться несколько монет, а какие-то клетки могли оказаться пустыми). Какие значения может принимать 𝑚? Укажите все возможные варианты.

