Задача 1.
Поменяйте местами две цифры, чтобы получилось верное равенство:

Задача 2.
У Пети на дне рождения был круглый торт, который резали прямолинейно через центр. На каждом куске было по свечке, а на одном куске ещё и розочка. Маша и Миша стали считать свечки по кругу (каждый начал со свечки), но оба забыли места, с которых начали. Маша насчитала 6 свечек и 2 розочки, а Миша – 19 свечек и 3 розочки. Сколько лет исполнилось Пете?
Комментарий: Пете столько лет, сколько свечек на торте. Рисунок ниже приведён для примера (может не совпадать с тортом Пети).
Задача 3.
Разрежьте клетчатую фигурку на рисунке ниже на две одинаковые части, каждая из которых является разверткой кубика 1×1×1.

Задача 4.
В таблице ниже расставьте числа от 1 до 7 так, чтобы в каждом столбце и каждой строчке, а также в каждой выделенной маленькой фигуре, были все семь чисел.
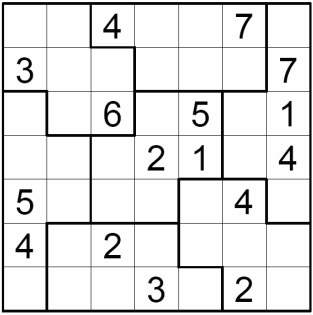
Задача 5.
У Никиты на линейке отмечены сантиметровые и миллиметровые деления. При этом Никита выяснил, что на линейке у него ровно 81 миллиметровое деление. Какое расстояние между первым и последним делением Никитиной линейки?
Комментарий: Первое деление, как и на всех линейках – сантиметровое – 0 см.

Задача 6.
У Винни-Пуха есть 11 больших горшков с мёдом и 10 маленьких. В магазине продаются коробки, в которые можно упаковать или 5 больших горшков, или 9 маленьких, или 4 больших и 3 маленьких. Сколько коробок придётся купить Винни, чтобы упаковать все свои горшки? (Он хочет купить как можно меньше коробок.)
Комментарий: Все коробки одинаковые. Другие способы упаковки Винни Пуху неизвестны. Вместо больших горшков можно класть маленькие или не наполнять коробки полностью. Все большие горшки одинаковы и все маленькие тоже одинаковы.
Задача 7.
На олимпиаду пришли Андрей, Боря и Витя. Один из них первоклассник, другой – второклассник, а третий – третьеклассник. Известно, что второклассник решил на одну задачу меньше, чем Андрей, а Витя решил на две задачи больше, чем третьеклассник. Кто решил больше задач и на сколько: Боря или первоклассник?
Задача 8.
У Саши есть 2 золотых, 3 серебряных и 4 бронзовых монеты. Одна из них фальшивая, причём, если фальшивая монета серебряная, то она легче настоящей серебряной, а если фальшивая золотая или бронзовая, то она тяжелее соответственно настоящей золотой или бронзовой. За два взвешивания на чашечных весах без гирь найдите фальшивую монету.
Примечание: Монеты из разного металла могут весить по-разному, однако настоящие монеты из одного металла весят одинаково.

