Задача 1.
Музей Сибирского федерального университета состоит из шести залов. Бельчонок начал осмотр с зала, показанного на рисунке, и закончил в нём же, пройдя все залы. Сколько различных маршрутов мог совершить бельчонок, если он прошёл в каждую дверь ровно один раз (в один и тот же зал можно заходить несколько раз)?
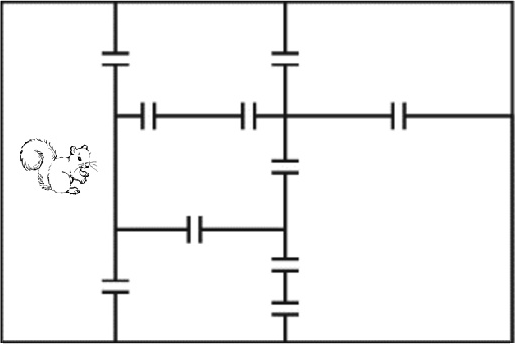
Задача 2.
В одном лесу росли дуб возрастом 180 лет и сосна возрастом 173 года. Через сколько лет возраст сосны будет составлять 99% от возраста дуба?
Задача 3.
В параллелограмме $KLMN$ (см. рисунок) отмечены точки $P$ и $Q$. Известно, что $\angle K L M$ = 110°, $\angle Q K N$ = $\angle P M N$ = 10°, $K Q$ = $K L$ и $P M$ = $L M$. Чему равна градусная мера $\angle P N Q$?
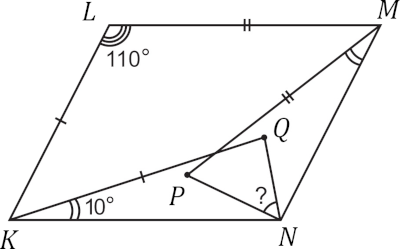
Задача 4.
Найдите сумму всех трёхзначных чисел $\overline{abc}$, делящихся нa 4‚ для которых $\displaystyle \frac{a}{b} = \frac{b}{c}$.
Задача 5.
Известно, что для действительных чисел $m$, $n$, $x$ и $y$ выполнены равенства $mx + ny = 3$, $my − nx = 4$ и $m^2 + n^2 = 1$. Какие значения может принимать выражение $x^2 + y^2$? Если значений несколько, то в ответ запишите их сумму.
Задача 6.
В прямоугольном треугольнике $ABC$ с прямым углом $B$ известно, что $BC$ = 5 ($BC$ < $AB$), На гипотенузе $AC$ отмечена точка $P$ так, что $AP$ = $AB$, а на катете $AB$ отмечена точка $Q$ так, что $PQ$ = $AQ$ = 6, Чему равен периметр четырёхугольника $CPQB$?
Задача 7.
В детском саду каждый ребёнок посчитал и написал нa бумажке два числа ($m$, $d$), где $m$ – количество мальчиков в его группе, а $d$ – количество девочек в его группе (самого себя ребёнок не считает). Оказалось, что на трёх бумажках было записано: (12;13), (15;10), (15;18). Сколько мальчиков и сколько девочек было в группе, если известно, что какое-то одно число записано правильно, а другое – отличается от правильного на 4.
Задача 8.
Бельчонок забыл пароль от сейфа, куда он спрятал орех. Он помнит, что паролем является четырёхзначное число $\overline{abcd}$, для которого верно равенство $\overline{dcba}$ − $\overline{abcd}$ = 7182, Какой же пароль от сейфа?
Задача 9.
Бельчонок раскладывает в 7 одинаковых кружков, отмеченных на сторонах и в центре равностороннего треугольника (см. рисунок) еловые и сосновые шишки, по одной в каждый кружок. Сколькими различными способами он сможет это сделать, если две расстановки, совпадающие при повороте треугольника, считаются одинаковыми?
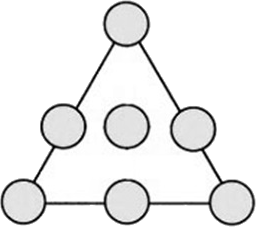
Задача 10.
Известно, что строитель Николай один может уложить кирпичную стену за 9 часов, а строитель Сергей один может уложить эту же стену – за 10 часов. Оба строителя укладывают одно и то же количество кирпичей за каждый час работы. Если бы Николай и Сергей работали сообща, то много бы разговаривали и за час укладывали бы вместе на 10 кирпичей меньше, чем могли бы. Сколько кирпичей необходимо, чтобы уложить стену, если Николай и Сергей вдвоём могут уложить стену за 5 часов?

