На рисунке изображён квадрат со стороной 42 см, который разрезан двумя прямыми, параллельными его сторонам, на три прямоугольника одинаковой площади. Найдите общую длину в сантиметрах двух проведённых разрезов.

По прямой дистанции в 1200 метров в одну сторону бегут бельчата Вася и Дима, а им навстречу – Петя. Все бельчата стартовали одновременно и движутся с постоянными скоростями (каждый со своей). В момент встречи Васи и Пети Дима пробежал всю дистанцию и был в 300 метрах от Васи. Сколько метров было между Васей и Димой в момент встречи Пети и Димы?

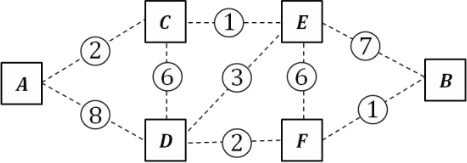
На схеме изображены 6 областей в лесу, соединенными прямыми дорогами, где живут бельчата. Стоимость прохода между областями в орехах указана на рисунке. За какое минимальное число орехов можно добраться из области A в область B?

Однажды на церемонии закрытия университетской олимпиады школьников «Бельчонок» по математике каждого победителя наградили трёмя подарками, каждого призёра II степени – двумя подарками, каждого призёра III степени – одним подарком. Председатель жюри заметил, что если бы победителям вручали по одному подарку, призёрам II степени – по 3 подарка, а призёрам III степени – по 2 подарка, то потребовалось бы ещё 17 подарков. Сколько учащихся суммарно стали призёрами II и III степеней, если победителей было 9?

Бельчонок нашёл в лесу 6 ящиков, причём только в одном находились орехи, а остальные ящики были пустыми.

• На первом ящике написано: «Орехи в третьем ящике».
• На втором: «Орехи во мне или в первом ящике».
• На третьем: «Во мне орехов нет».
• На четвёртом: «Орехи лежат в ящике с нечётным номером».
• На пятом: «Во втором и шестом ящике орехов нет».
• На шестом: «В четвёртом ящике орехов нет».

Известно, что среди надписей три истинных и три ложных. В каком ящике лежат орехи? В ответе укажите номер ящика.

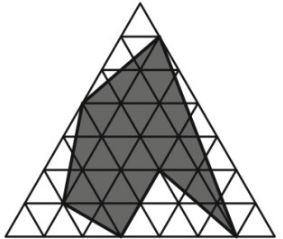
Найдите площадь закрашенной фигуры, изображённой на рисунке, если известно, что площадь одного маленького треугольника равна 1 см². Ответ дайте в квадратных сантиметрах.

В числовом ребусе ABCD + ABCD = EFDGB одинаковыми буквами обозначены одинаковые цифры, разными буквами — разные цифры. Какое наибольшее число может соответствовать слову EFDGB?

Учитель записал на доске несколько различных натуральных двузначных чисел. Шестиклассники получили следующее задание: Вера стирает с доски все числа, делящиеся на 2, Гена – делящиеся на 3, Даша – делящиеся на 5, а Женя – делящиеся на 7. Ребята выполняли задание по очереди, но неизвестно в каком порядке. В результате Вера стёрла числа 32 и 56, Гена – 24, 33, 45, Даша – 20, 25 и 35. Какие три числа стёр Женя? В ответ запишите сумму этих чисел.

Бельчата Таша и Яша искали орехи и похвастались друг другу, кто сколько нашёл. При этом Таша преувеличила количество найденных орехов в 2 раза, Яша – в 7 раз, а в сумме получилось втрое больше орехов, чем на самом деле. Кто нашёл больше орехов и во сколько раз?

В клетках квадрата 30×30 лежат орехи (в каждой клетке – не более одного ореха). Оказалось, что в любом прямоугольнике 1×2 лежит хотя бы один орех, а в каждом прямоугольнике 1×6 есть две клетки с орехами, стоящие рядом. Какое наименьшее количество орехов может находиться в этом квадрате?