Задача 1.
Известно, что для действительных чисел $a$, $b$, $c$ выполнены равенства:
$$ \frac{1}{a} + \frac{7}{b} = \frac{5}{c} $$
$$ \frac{7}{a} + \frac{1}{b} = \frac{11}{c} $$
$$ \frac{a+b}{5} = \frac{3}{c} $$
Какие значения может принимать выражение $a + b + c$?
Если значений несколько, то в ответ запишите их сумму.
Задача 2.
В пенале лежат 7 красных ручек, 15 чёрных ручек, 19 красных карандашей и 8 чёрных карандашей. Какое минимальное количество предметов нужно вынуть из пенала не глядя, чтобы среди них наверняка оказались ручка и карандаш одинакового цвета?
Задача 3.
На доске нарисованы квадраты со сторонами 1, 2, 3, 4, 5, 6, 7, 8 и 9 см по порядку так, чтобы вершина каждого следующего квадрата совпала с центром предыдущего (см. рисунок). Какова площадь доски, покрытая квадратами?
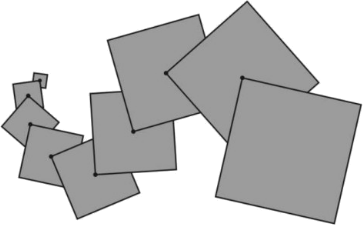
Задача 4.
Натуральное число $n$ удовлетворяет условиям НОК($n$, 100 ) = 700, НОК($n + 2$, 100) = 300. Чему может равняться НОК($n + 1$, 100)? Если ответов несколько, то в ответ запишите их сумму.
Задача 5.
Двое снегоуборщиков очищали территорию Сибирского федерального университета от снега. После того как первый проработал 3 часа, а второй – 7 часов, оказалось, что они выполнили 40% всей работы. Проработав совместно ещё 5 часов, они осознали, что им осталось выполнить ещё $\displaystyle \frac{6}{35}$ всей работы. За сколько часов, работая отдельно, каждый из них мог бы очистить эту территорию? В ответ запишите произведение полученных чисел.
Задача 6.
Прямоугольник поделён на 5 частей так, как показано на рисунке. Каждую из частей можно раскрасить одним из четырёх цветов: красным, жёлтым, синим или оранжевым. Сколькими способами можно раскрасить эти части, если известно, что никакие две граничащие части не должны быть покрашены в одинаковый цвет? (Все четыре цвета использовать необязательно.)
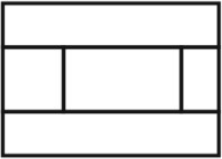
Задача 7.
Из трёх цифр С , Ф и У составили два шестизначных числа СФУСФУ и СФСФСФ , которые относятся друг к другу как 55:54. Чему равняется число СФУ?
Задача 8.
У бельчонка есть 100 орехов, к которым прикреплены бумажки с номерами от 100 до 199. Вчера он выложил эти орехи в ряд в порядке возрастания их номеров. Сегодня он поменял местами некоторые орехи так, чтобы номера любых двух соседних орехов отличаются ровно одной цифрой, а разность номеров соседних орехов равняется 1 или 10. Какое наибольшее количество орехов могло остаться на своих местах?
Задача 9.
В пятиугольнике PQRST известно, что PQ = QR = RS = ST , ∠Q = 96° и ∠R = ∠S = 108°. Чему равна градусная мера ∠T?
Задача 10.
Дана клетчатая доска 10×10, каждую клетку которой необходимо покрасить в серый или оранжевый цвета. Назовём клетку «отличной», если у неё хотя бы семь соседних клеток не такого, как она, цвета. Какое наибольшее количество «отличных» оранжевых клеток может быть одновременно на доске? (Клетки называются соседними, если они имеют общую сторону или общий угол.)

