Задача 1.
Известно, что для корней квадратного трёхчлена x2 + ax + b квадрат их суммы на 30 больше суммы их квадратов. Найдите значение коэффициента b.
Задача 2.
В конкурсе по поиску орехов в лесу около Сибирского федерального университета принимали участие 24 бельчонка. Каждому из них достался порядковый номер от 1 до 24. Однако в связи с повышенной температурой один бельчонок не смог участвовать в конкурсе. Оказалось, что среди 23 оставшихся бельчат нашёлся один, номер которого равнялся среднему арифметическому номеров оставшихся 22 бельчат. Какой номер имел бельчонок, не допущенный до соревнований? Если значений несколько, то в ответ запишите их сумму.
Задача 3.
Из города Мышкино в город Кошкино по расписанию движется поезд со скоростью 60 км/ч. В какой-то момент он останавливается на светофоре и стоит там 3 минуты. После этого он продолжает движение со скоростью 75 км/ч и прибывает в Кошкино точно по расписанию. За сколько километров до Кошкино поезд остановился на светофоре?
Задача 4.
В слове «БУКИНИСТ» одинаковыми буквами обозначены одинаковые цифры, разными буквами – разные цифры. Сколько существует таких слов, если дополнительно известно, что Т > С > И < Н и К < У < И < Б?
Задача 5.
На гипотенузе PQ и катете PR прямоугольного треугольника PQR внешним образом построены прямоугольные треугольники PQN и PRM так, что ∠PNQ = ∠PMR = 90°, ∠PQN = ∠PRM = 60°. На стороне QR взята точка T так, что QT = TR. Найдите градусную меру ∠MTN.
Задача 6.
Известно, что для действительных чисел a, b выполнены равенства: a + 4 = (b − 2)2, b + 4 = (a − 2)2. Какие значения может принимать выражение a2 + b2? Если значений несколько, то в ответ запишите их сумму.
Задача 7.
Юный химик Миша из цистерны объёмом 1000 литров, наполненной водным раствором некоторого вещества, вылил несколько литров жидкости, долил цистерну водой, потом вылил в два раза большее количество жидкости и опять долил цистерну водой. После этого оказалось, что количество вещества в цистерне уменьшилось в 25/3 раза. Сколько литров жидкости вылил Миша в первый раз?
Задача 8.
50 жителей племени Сиу и 50 жителей племени Тиу подошли к реке, у которой находилась шлюпка. Известно, что шлюпка выдерживает 300 кг и имеется всего одна пара весел. Грести умеют все, однако любой житель племени Сиу может грести, только если в шлюпке кроме него никого нет. Кроме того, любой житель племени Сиу не согласен наедине оставаться или плыть с жителями племени Тиу. Какое наименьшее количество часов необходимо, чтобы все жители переправились на другой берег реки, если одна переправа занимает 30 минут, каждый житель племени Сиу весит 50 кг, а каждый житель племени Тиу – 110 кг.
Задача 9.
На окружности отмечены точки P, Q, R так, что PQ = 9, PR = 8, QR = 6. Прямая TR касается окружности и TR = 12. Найдите длину PT. В ответе укажите число, умноженное на 4,5.
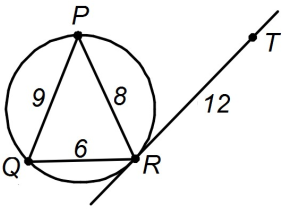
Задача 10.
Петя изучает программирование и для тренировки написал программу, которая для натуральных чисел x, y выводит на экран НОД(x2 − 3, y2 − x, y − 3). Какое наибольшее число может появиться на экране?

