Задача 1.
Софи рисует цветных кенгуру: сначала голубого, потом зелёного, потом красного, потом чёрного, снова голубого, зелёного, красного, чёрного и так далее... Какого цвета будет двадцать шестой кенгуру?
(А) голубого
(Б) зелёного
(В) красного
(Г) чёрного
(Д) жёлтого
Задача 2.
$\displaystyle \frac{2003 + 2003 + 2003 + 2003 + 2003}{2003 + 2003}$ = ?
(А) 2003
(Б) 1/3
(В) 3
(Г) 5/2
(Д) 6009
Задача 3.
Сумма чисел в каждом из колец равна 55. Чему равно число А?
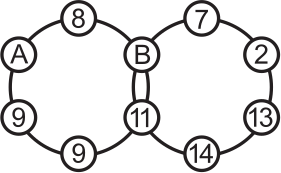
(А) 9
(Б) 10
(В) 13
(Г) 16
(Д) 17
Задача 4.
Возьмем самое маленькое число, которое делится на 2 и на 3, и самое маленькое число, которое делится на 2, 3 и 4. Их сумма равна
(А) 9
(Б) 32
(В) 20
(Г) 24
(Д) 18
Задача 5.
На листок клетчатой бумаги требуется уложить квадрат со стороной, равной 2,5 клеткам, так, чтобы он закрыл как можно больше целых клеток. Число полностью закрытых клеток при этом будет равно
(А) 2
(Б) 3
(В) 4
(Г) 6
(Д) 8
Задача 6.
На рисунке изображены два одинаковых стакана, в которые налито одинаковое количество воды. Чему равна высота уровня воды х, если высота стакана равна 10 см?
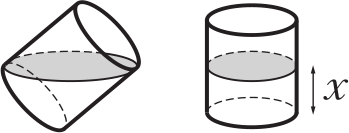
(А) 3 см
(Б) 4 см
(В) 5 см
(Г) 6 см
(Д) 7 см
Задача 7.
Серёжа любит подсчитывать сумму цифр на табло электронных часов. Например, если часы показывают 21:17, Серёжа получает число 11. Какую наибольшую сумму он может получить?
(А) 19
(Б) 23
(В) 24
(Г) 25
(Д) 36
Задача 8.
Из набора чисел 1, 2, …, 17 вычеркнуты все чётные числа, а также все такие числа 𝑥, что 17 − 𝑥 делится на 3. Сколько чисел осталось?
(А) 4
(Б) 5
(В) 6
(Г) 7
(Д) 8
Задача 9.
На рисунке АС = 10 см, ВD = 15 см и АD = 22 см. Чему равно ВС?
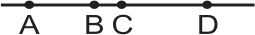
(А) 3 см
(Б) 5 см
(В) 7 см
(Г) 9 см
(Д) 12 см
Задача 10.
Сколько треугольников на этом рисунке имеют такую же площадь, как и целая клетка?
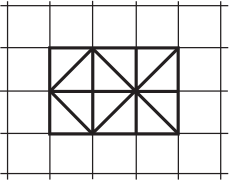
(А) 2
(Б) 4
(В) 6
(Г) 7
(Д) 10
Задача 11.
Сколько различных результатов можно получить, складывая по два различных числа из набора 1, 2, 3, 4 и 5?
(А) 5
(Б) 6
(В) 7
(Г) 8
(Д) 9
Задача 12.
Штрих-код образован 17 чёрными и белыми полосками (крайние полоски — чёрные). Черные полоски бывают двух типов: узкие и широкие. Число белых полосок на 3 больше, чем число широких чёрных. Чему равно число узких чёрных полосок?

(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 13.
Прямоугольник составлен из 7 квадратов. Сторона чёрного квадрата равна 1, а сторона серого квадрата равна 3. Чему равна площадь квадрата А?
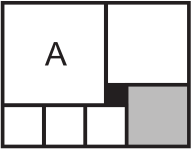
(А) 16
(Б) 25
(В) 36
(Г) 49
(Д) это невозможно сделать
Задача 14.
Число B записывается одними единицами – всего 2003 цифр. Сколько цифр содержит произведение числа B на 2003?
(А) 2003
(Б) 2004
(В) 2006
(Г) 4006
(Д) 20032
Задача 15.
Прямоугольный параллелепипед с размерами 1 × 1 × 2 склеен из бумаги. Какая из нарисованных фигурок может получиться, если этот параллелепипед разрезать по каким-то рёбрам и развернуть? (Клетки на рисунках имеют размер 1 × 1).
(А) 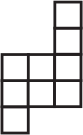
(Б) 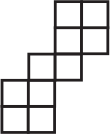
(В) 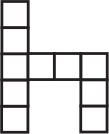
(Г) 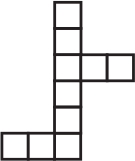
(Д) 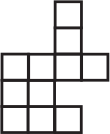
Задача 16.
В прямоугольнике размером 200 × 300, нарисованном на клетчатой бумаге, провели диагональ. Сколько клеточек она разрезала на две части?
(А) 300
(Б) 356
(В) 400
(Г) 450
(Д) 512
Задача 17.
Заяц соревновался с черепахой в беге на 100 метров. Когда заяц прибежал к финишу, черепахе оставалось до него ещё 90 метров. На сколько метров надо отодвинуть назад стартовую линию для зайца, чтобы при новой попытке оба бегуна пришли к финишу одновременно?
(А) 90
(Б) 100
(В) 10
(Г) 900
(Д) 1000
Задача 18.
В числовом ребусе различным буквам соответствуют различные цифры, а одинаковым буквам – одинаковые цифры. Этот ребус имеет много решений. Какая наибольшая цифра может быть зашифрована буквой У?

(А) 5
(Б) 6
(В) 7
(Г) 8
(Д) 9
Задача 19.
Лиза выбрала двузначное число, не делящееся на 10, поменяла его цифры местами и вычислила разность полученных чисел. Какое самое большое число она могла получить?
(А) 90
(Б) 81
(В) 75
(Г) 72
(Д) 45
Задача 20.
Лёша и Гоша вскапывали на огороде грядку. Они начали работу с противоположных концов грядки, двигаясь навстречу друг другу. Гоша копал в два раза быстрее, чем Лёша, но зато после каждого вскопанного метра устраивал перерыв на 20 минут, а Лёша копал хоть и медленно, но без перерывов. Через 2 часа после начала работы Лёша добрался до середины грядки и обнаружил там выполнившего свою половину работы Гошу. Чему равна длина грядки?
(А) 3 м
(Б) 6 м
(В) 9 м
(Г) 12 м
(Д) не хватает данных
Задача 21.
Из листа клетчатой бумаги вырезали два куска. В результате образовалась дыра, изображённая на правом рисунке. Найдите вырезанные куски среди фигур 1-4.
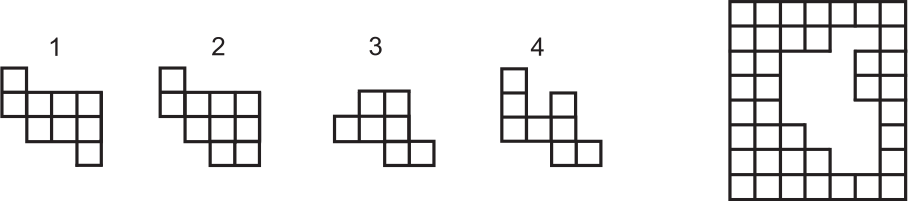
(А) 1 и 3
(Б) 2 и 4
(В) 2 и 3
(Г) 1 и 4
(Д) это невозможно
Задача 22.
Имеется 6 палочек, длины которых равны 1 см, 2 см, 3 см, 2001 см, 2002 см и 2003 см. Надо выбрать три палочки и составить из них треугольник. Каким числом способов можно подобрать подходящие тройки палочек?
(А) 1
(Б) 3
(В) 5
(Г) 6
(Д) более 50
Задача 23.
Костя Сергеев из 5А класса и 8 его друзей из той же школы отправились в поход. Оказалось, что среди любых четырёх из этих туристов обязательно есть одноклассники, а среди любых пяти — не больше, чем три одноклассника. Сколько учеников 5А класса пошли в поход?
(А) 2
(Б) 3
(В) 4
(Г) 1
(Д) невозможно определить
Задача 24.
За год поголовье кенгуру в австралийском заповеднике выросло на 10%, а потом 9,5% всех кенгуру отправились на поиски лучшего корма на соседние пастбища. В результате количество кенгуру в заповеднике
(А) выросло на 0,5%
(Б) не изменилось
(В) уменьшилось на 0,5%
(Г) выросло на 0,45%
(Д) уменьшилось на 0,45%
Задача 25.
Каким числом способов можно замостить белую клетчатую часть нарисованной фигуры плитками размера 2 × 1?

(А) 1
(Б) 2
(В) 4
(Г) 8
(Д) 16
Задача 26.
На плоскости отметили 10 точек, затем каждые две из них соединили отрезком. Какое наибольшее число таких отрезков может пересечь прямая, которая не проходит ни через одну их этих точек?
(А) 20
(Б) 25
(В) 30
(Г) 35
(Д) 45
Задача 27.
Четыре девочки поют песни, аккомпанируя друг другу. Каждый раз одна из них играет, а остальные три поют. Оказалось, что Анна спела больше всех песен — восемь, а Дороти спела меньше всех — пять. Сколько всего песен спели девочки?
(А) 12
(Б) 11
(В) 10
(Г) 9
(Д) невозможно определить
Задача 28.
Маша старше Миши ровно на один месяц (дни их рождения приходятся на одно и то же число в двух соседних месяцах), а Даша старше Миши на столько же дней, на сколько Маша старше Даши. В каком месяце не могла родиться Даша?
(А) в апреле
(Б) в мае
(В) в июне
(Г) в июле
(Д) в августе
Задача 29.
Назовем старшим делителем числа самый большой из его делителей, не равный самому числу, а младшим делителем назовём самый маленький делитель, не равный 1. Например, у числа 12 старший делитель равен 6, а младший — 2. Сколько существует чисел, у которых старший делитель в 15 раз больше младшего?
(А) 0
(Б) 1
(В) 2
(Г) 5
(Д) бесконечно много
Задача 30.
В десятичной записи числа 59876 использованы 5 последовательных цифр. Чему равна третья цифра следующего пятизначного числа, обладающего таким же свойством?
(А) 3
(Б) 4
(В) 5
(Г) 6
(Д) 7

