Задача 1.
В слове КЕНГУРУ стёрли 4 буквы (может быть, среди них были одинаковые). Оставшиеся буквы переписали в обратном порядке. Что могло получиться?
(А) РУГУ
(Б) УГУ
(В) РКУ
(Г) РУН
(Д) ГЕН
Задача 2.
2007 : (2 + 0 + 0 + 7) − 2 × 0 × 0 × 7 = ?
(А) 1
(Б) 9
(В) 214
(Г) 223
(Д) 2007
Задача 3.
Прямоугольник, расчерченный на клеточки, разрезали на две части. Одна из этих частей изображена ниже. Укажите вторую часть.
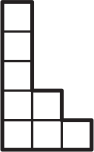
(А) 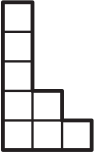
(Б) 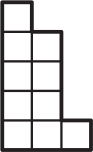
(В) 
(Г) 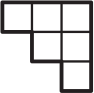
(Д) 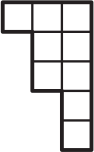
Задача 4.
Сейчас коту Тоше 10 лет и он в 5 раз старше кота Малыша. Через сколько лет Малышу будет 10 лет?
(А) 4
(Б) 5
(В) 6
(Г) 7
(Д) 8
Задача 5.
Чему не равно число 5?
(А) Стороне квадрата из 25 клеточек.
(Б) Номеру задачи, которую ты сейчас решаешь.
(В) Количеству баллов за самую трудную задачу конкурса «Кенгуру».
(Г) Количеству точек, которые делят окружность на 5 частей.
(Д) Количеству различных букв в слове МАТЕМАТИКА.
Задача 6.
Робот начинает двигаться из клетки А2 в направлении, указанном стрелкой. Он идёт только вперёд, пока не встречает закрашенную клетку или границу доски. Тогда он поворачивает направо на 90°. Если ни вперёд, ни вправо двигаться нельзя, робот останавливается. Где он остановится?
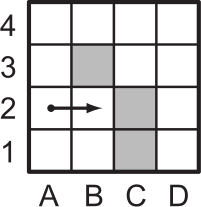
(А) В2
(Б) А1
(В) Е1
(Г) D1
(Д) робот не остановится никогда
Задача 7.
Каждое из 4 чисел больше 5 и меньше 9. Тогда их сумма может равняться
(А) 15
(Б) 18
(В) 20
(Г) 30
(Д) 45
Задача 8.
Если куб с ребром 1 метр разрезать на кубики с ребром 1 дециметр, и поставить эти кубики друг на друга, то получится «башня» высотой
(А) 1 м
(Б) 100 м
(В) 1 км
(Г) 10 км
(Д) 10 м
Задача 9.
Вася старше Пети ровно на один год без одного дня. Вася родился 1 января 2002 года. Когда родился Петя?
(А) 2 января 2003 года
(Б) 2 января 2001 года
(В) 31 декабря 2000 года
(Г) 31 декабря 2002 года
(Д) 31 декабря 2003 года
Задача 10.
Костя сложил несколько целых положительных чисел, а потом вычислил их среднее арифметическое. Оказалось, что сумма равна 50, а среднее арифметическое равно 10. Сколько чисел складывал Костя?
(А) 4
(Б) 5
(В) 8
(Г) 10
(Д) 25
Задача 11.
В каждую клетку таблицы 3 × 3 надо вписать цифры: 1, 2 или 3. Каждая цифра должна встречаться в каждой строчке и в каждом столбце. Первые три клетки уже заполнены. Сколькими способами можно завершить это задание?
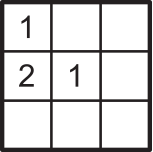
(А) 0
(Б) 1
(В) 2
(Г) 3
(Д) 4
Задача 12.
Андрей, Вася и Серёжа менялись марками: Вася отдал Серёже 5 своих марок, Серёжа отдал Андрею 4 марки, и Андрей отдал Васе 2 марки. В результате марок у всех троих мальчиков стало поровну. Сколько марок было у Андрея сначала, если всего у троих друзей 30 марок?
(А) 8
(Б) 9
(В) 11
(Г) 13
(Д) 15
Задача 13.
Число $\displaystyle \left(1 + \frac{1}{2}\right)\left(1 − \frac{1}{3}\right)\left(1 + \frac{1}{4}\right)\left(1 − \frac{1}{5}\right)\left(1 + \frac{1}{6}\right)\left(1 − \frac{1}{7}\right)\left(1 + \frac{1}{8}\right)\left(1 − \frac{1}{9}\right)$ равно
(А) $\displaystyle \frac{1}{10}$
(Б) $\displaystyle \frac{9}{10}$
(В) $\displaystyle \frac{7}{15}$
(Г) $\displaystyle \frac{25}{36}$
(Д) 1
Задача 14.
Квадрат разбит на одинаковые клетки, раскрашенные в шахматном порядке в чёрный и белый цвета. Число чёрных клеток равно 25. Сколько клеток в стороне квадрата?
(А) 4
(Б) 5
(В) 6
(Г) 7
(Д) 8
Задача 15.
Фигура А составлена из четырёх полосок бумаги. Каждая полоска на 1 см длиннее той, которая примыкает к ней слева. Фигура В составлена из точно таких же полосок, но в другом порядке. Тогда периметр фигуры А меньше периметра фигуры В на
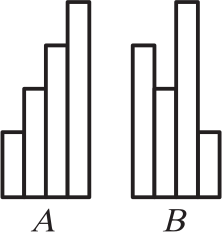
(А) 1 см
(Б) 2 см
(В) 3 см
(Г) 4 см
(Д) периметры этих фигур равны
Задача 16.
Жан-Кристоф продолжает изучать русский язык. Он обнаружил, что есть двузначные числа с интересным свойством: такое число читается в два слова, но если его цифры переставить, то новое число будет читаться в одно слово. Сколько таких чисел?
(А) 3
(Б) 6
(В) 8
(Г) 9
(Д) 10
Задача 17.
Отрезок АВ пересечён ломаной линией, как показано на рисунке. При этом получилось 5 квадратов. Чему равна длина ломаной АА1А2… А10B, если длина АВ равна 10 см?
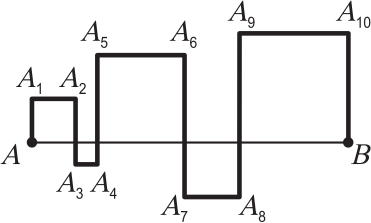
(А) 30 см
(Б) 40 см
(В) 50 см
(Г) 60 см
(Д) 80 см
Задача 18.
Человек Рассеянный с улицы Бассейной уверен, что его часы спешат на 30 минут, а на самом деле они отстают на 20 минут. Он торопится на поезд, который отправляется в 20 часов 20 минут. В какое время прибежал он на перрон (и сел в отцепленный вагон), если ему кажется, что он пришёл точно к отправлению?
(А) 19 часов 50 минут
(Б) 20 часов 50 минут
(В) 21 час 00 минут
(Г) 21 час 10 минут
(Д) 21 час 30 минут
Задача 19.
На рисунке изображён бумажный кубик. Какая из фигурок может получиться, если его разрезать вдоль каких-то рёбер и расправить?

(А) 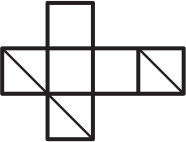
(Б) 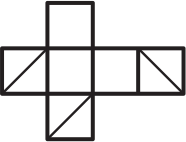
(В) 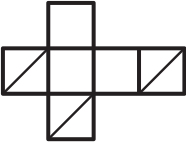
(Г) 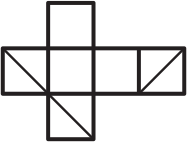
(Д) ни один из вариантов А-Г не получится
Задача 20.
Какой самый большой результат может получиться, если в выражении ЗА + ДАЧ + КА заменить каждую букву какой-то цифрой (разные буквы заменяются разными цифрами)?
(А) 1131
(Б) 1129
(В) 1127
(Г) 1125
(Д) невозможно определить
Задача 21.
У скольких двузначных чисел при умножении на 2 не меняется сумма цифр?
(А) 5
(Б) 8
(В) 10
(Г) 16
(Д) таких чисел нет
Задача 22.
Когда в школе объявили день вежливости, каждый мальчик из 5А класса поздоровался за руку с каждой девочкой из своего класса. Всего при этом было 77 рукопожатий. Сколько учеников может быть в 5А классе?
(А) 16
(Б) 17
(В) 18
(Г) 19
(Д) 22
Задача 23.
Сумма двух положительных дробей равна 41/65. Чему равен числитель большей из этих дробей, если их знаменатели меньше 65?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 24.
Буратино увидел двух продавцов с тетрадками по одной и той же цене.
«Умненький Буратино, – зовет его один продавец – если ты купишь у меня две тетрадки, то я их обе продам тебе на 40% дешевле!».
«Богатенький Буратино, – кричит другой – если ты купишь такую же тетрадку у меня по обычной цене, то вторую я продам всего за 20 сольдо!».
Умница Мальвина подсказала Буратино, что покупка двух тетрадок у первого продавца обойдётся на 5 сольдо дешевле, чем у второго. Сколько стоила одна тетрадка сначала?
(А) 20
(Б) 40
(В) 60
(Г) 75
(Д) 90
Задача 25.
По кругу написаны 5 целых чисел, причём сумма никаких двух соседних и никаких трёх идущих подряд чисел не делится на 3. Сколько из написанных чисел делятся на 3?
(А) 0
(Б) 1
(В) 2
(Г) 3
(Д) невозможно определить
Задача 26.
С какой цифры начинается самое маленькое натуральное число, у которого произведение цифр равно 120?
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 27.
На праздник к Анне и Берте пришли гости. Оказалось, что Анна знает 80% гостей, а Берта – 60%. Каждый гость знаком хотя бы одной из этих девочек, а 6 человек знакомы им обеим. Сколько гостей было на празднике?
(А) 5
(Б) 10
(В) 15
(Г) 20
(Д) 25
Задача 28.
Общее количество точек на противоположных гранях игрального кубика равно 7. Четыре одинаковых игральных кубика сложили вместе и закрасили некоторые грани. Сколько точек было на грани, отмеченной знаком ∗, если кубики приложены друг к другу по одинаковым граням?
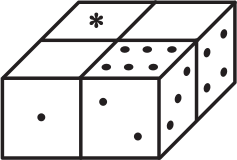
(А) 5
(Б) 3
(В) 2
(Г) 1
(Д) нельзя определить
Задача 29.
В примере на умножение КЕН × ГА = 7632 использованы все цифры от 1 до 9, каждая по одному разу. Какую цифру заменяет буква Е?
(А) 1
(Б) 4
(В) 5
(Г) 8
(Д) 9
Задача 30.
Тимофей резал бумажный треугольник на кусочки (все разрезы — прямые). Сначала он разрезал этот треугольник на две части. Потом разрезал на два куска одну из полученных частей, и так далее. Когда ему надоело резать, оказалось, что общее количество углов у всех получившихся фигур равно 2007. Какое наименьшее количество разрезов мог сделать Тимофей?
(А) 2007
(Б) 1002
(В) 668
(Г) 501
(Д) так разрезать нельзя

