Задача 1.
Сколько острых углов в 2009 тупоугольных треугольниках?
(А) 0
(Б) 2009
(В) 4018
(Г) 6027
(Д) невозможно определить
Задача 2.
Если $\left(3^3\right)^x$ = 99, то x равен
(А) 2
(Б) 3
(В) 4
(Г) 6
(Д) 9
Задача 3.
Кольцами Борромео называется система из трёх колец с таким свойством: эта система не распадается, но если любое из колец распилить и убрать, то два других окажутся несцепленными. Какие из систем на рисунке являются кольцами Борромео?
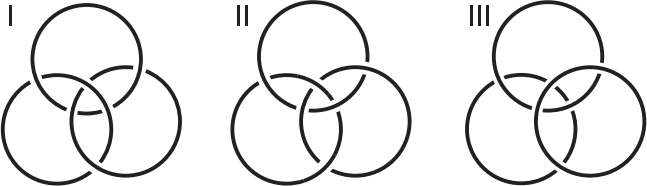
(А) I
(Б) II
(В) III
(Г) ни одна
(Д) все три
Задача 4.
В последовательности чисел каждый член, начиная с третьего, равен сумме двух предыдущих. Четвертый член равен 6, а шестой равен 15. Чему равен седьмой член этой последовательности?
(А) 9
(Б) 16
(В) 21
(Г) 22
(Д) 24
Задача 5.
Вася сказал: «Уравнения бывают линейные, прямолинейные, криволинейные, квадратные, треугольные, кубические и шарообразные». Сколько несуществующих типов уравнений он назвал?
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 6.
В треугольнике PQR на стороне QR отмечена точка S так, что ∠QPS = 12°, PQ = PS = RS. Чему равен ∠QRP ?
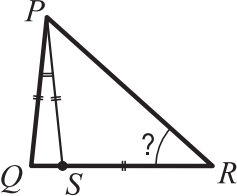
(А) 36º
(Б) 42º
(В) 54º
(Г) 60º
(Д) 84º
Задача 7.
В слове КЕНГУРУ поменяли местами две соседние буквы, в полученном «слове» опять переставили две соседние буквы, и в том «слове», что получилось, проделали это ещё раз. Что не могло получиться в итоге?
(А) КУГЕРУН
(Б) ЕНКГУУР
(В) КЕГУРНУ
(Г) КНЕУГУР
(Д) КЕГНУРУ
Задача 8.
Через 5 часов наверняка уже будет «завтра». Сколько часов назад наверняка было «вчера»?
(А) 18
(Б) 20
(В) 30
(Г) 44
(Д) 47
Задача 9.
У некоторых натуральных чисел квадрат и куб записываются одинаковым количеством цифр. Сколько таких чисел?
(А) 0
(Б) 3
(В) 4
(Г) 9
(Д) бесконечно много
Задача 10.
Числа a, b и c таковы, что a : b : c равно 1 : 2 : 3. Чему равно (a + b) : (b + c) : (c + a) ?
(А) 2 : 3 : 4
(Б) 3 : 5 : 4
(В) 3 : 5 : 6
(Г) 4 : 6 : 5
(Д) 2 : 6 : 5
Задача 11.
Центры непересекающихся окружностей радиуса 2 расположены в вершинах треугольника. Какова сумма площадей трёх закрашенных секторов?
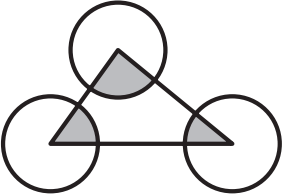
(А) π
(Б) 2π
(В) 4π
(Г) 8π
(Д) невозможно определить
Задача 12.
Когда большой бриллиант раскололи на 2 части, его общая стоимость упала на 48%, Какую долю всего бриллианта составляет его большая часть, если стоимость бриллианта пропорциональна квадрату массы?
(А) 2/3
(Б) 3/4
(В) 4/5
(Г) 3/5
(Д) 4/7
Задача 13.
Коля обвёл на глобусе красной краской экватор и ещё две окружности, проходящие через нулевой и 90-й меридианы. Муха села в точку пересечения двух красных окружностей и поползла по одной из них. В ближайшей точке пересечения двух окружностей она повернула направо, потом (в следующей точке пересечения) налево, потом опять направо, и т.д., пока не вернулась в исходную точку. Сколько поворотов сделала муха?
(А) 12
(Б) 10
(В) 8
(Г) 7
(Д) 5
Задача 14.
На выборах мэра Цветочного города выдвинуто две кандидатуры: Знайка и Незнайка. Когда избирательная комиссия обработала n% всех бюллетеней, оказалось, что Знайка получил 62% голосов, а Незнайка — 38% (от обработанных бюллетеней). При каком наименьшем натуральном значении n можно быть уверенным, что Знайка набрал больше половины всех голосов, если недействительных бюллетеней нет?
(А) 79
(Б) 80
(В) 81
(Г) 82
(Д) 83
Задача 15.
Сколько нулей нужно написать вместо ∗ в десятичной дроби 1.∗1, чтобы получить число, лежащее между $\displaystyle \frac{209}{208}$ и $\displaystyle \frac{2009}{2008}$ ?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 16.
Из данных векторов Вася выбирает несколько и находит их сумму. Какова длина самого длинного вектора, который он может получить, если сторона клетки равна 1?
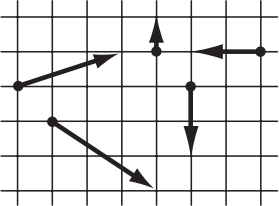
(А) 2√13
(Б) 6√2
(В) √65
(Г) 3√5
(Д) 10
Задача 17.
Ордината вершины параболы y = x2 + bx + c равна −7. Известно, что c < 0. Какое из чисел не может лежать между корнями уравнения x2 + bx + c = 0 ?
(А) −5
(Б) −3
(В) 1
(Г) 5
(Д) 6
Задача 18.
В двух треугольниках, остроугольном и тупоугольном, измерили углы. Вот величины четырёх из них: 110º, 75º, 65º, 15º. Чему равен меньший угол остроугольного треугольника?
(А) 10º
(Б) 15º
(В) 40º
(Г) 45º
(Д) невозможно определить
Задача 19.
Если $a^3 + 7a − 9 = 0$, то число $\displaystyle \frac{2a^3 + 3a}{11a − 18}$ равно
(А) −1
(Б) $\displaystyle −\frac{1}{2}$
(В) $\displaystyle \frac{1}{2}$
(Г) 1
(Д) невозможно определить
Задача 20.
Два различных трёхзначных числа назовём родственниками, если для их записи используется один и тот же набор цифр. Например, 244 и 424 — родственники, а 244 и 224 — нет. Сколько родственников не бывает у трёхзначного числа с суммой цифр 5?
(А) 0
(Б) 1
(В) 2
(Г) 3
(Д) любое из чисел 0, 1, 2 и 3 возможно
Задача 21.
Пусть a1 = 2 и an + 1 $\displaystyle = \frac{a_n − 1}{a_n + 1}$. Чему равно a2009 ?
(А) 2
(Б) 1/3
(В) −1/2
(Г) −3
(Д) другой ответ
Задача 22.
Кенгуру прыгает по координатной плоскости. Каждый его прыжок параллелен одной из координатных осей и имеет длину 1. Сколько на плоскости точек, в которых Кенгуру может оказаться, сделав ровно 10 прыжков, если он стартует из начала координат?
(А) 100
(Б) 121
(В) 400
(Г) 441
(Д) другой ответ
Задача 23.
Про треугольник АВС известно, что АВ = 5, ВС = 11, а угол В в два раза больше, чем угол С. Чему равно АС ?
(А) 4√5
(Б) 4√3
(В) 3√5
(Г) 5√2
(Д) другой ответ
Задача 24.
Таблицу 3 × 3 заполнили числами так, что суммы чисел в каждой строке, каждом столбце и на обеих диагоналях равны 3. Тогда обязательно
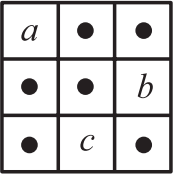
(А) a + b + c = 3
(Б) a = $\displaystyle = \frac{b + c}{2}$
(В) a + b + c = 0
(Г) a = b + c
(Д) любое из условий А-Г может нарушаться
Задача 25.
На плоскости заданы прямые y = ax − 1 и y = x + b . Известно, что первая прямая пересекает ось Ох правее, чем вторая, а ось Оу — выше, чем вторая. Какое из неравенств может быть неверным?
(А) a > 0
(Б) ab > −1
(В) a < 1
(Г) a + b < 0
(Д) все неравенства А-Г обязательно верны
Задача 26.
Из точки А на рисунке можно «увидеть» лишь 5 из 9 квадратов (остальные 4 квадрата целиком загорожены этими пятью). Какое наибольшее число квадратов можно увидеть, выбрав другую точку обзора на той же плоскости?
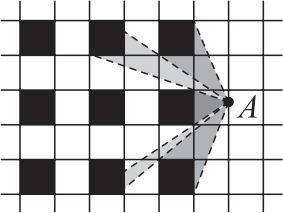
(А) 5
(Б) 6
(В) 7
(Г) 8
(Д) 9
Задача 27.
Два человека начали одновременно спускаться по движущемуся вниз эскалатору. Первый идёт вдвое быстрее, чем второй. Сколько ступенек на эскалаторе, если к концу спуска первый прошёл 60 ступенек, а второй — 40?
(А) 80
(Б) 100
(В) 120
(Г) 140
(Д) другой ответ
Задача 28.
Маша загадала натуральное число и выписала в строчку подряд в порядке возрастания все его делители, кроме самого этого числа (например, для числа 14 она написала бы число 127). Какое число при этом не могло получиться?
(А) 1237
(Б) 12346
(В) 123612
(Г) 124816
(Д) 111121
Задача 29.
Назовём прямоугольный параллелепипед хорошим, если его можно разрезать на два равных прямоугольных параллелепипеда, имеющих хотя бы по одной квадратной грани. Сколько существует хороших прямоугольных параллелепипедов, имеющих грань 2 × 6?
(А) 2
(Б) 4
(В) 5
(Г) 6
(Д) 8
Задача 30.
В некотором треугольнике измерили три высоты. Какая тройка чисел могла получиться?
(А) 1, 2, 3
(Б) 4, 7, 8
(В) 3, 6, 8
(Г) 2, 4, 5
(Д) 5, 10, 11

